5521
Density Weighted Concentric Circle Trajectories for Brain MRSI at 7T1High Field MR Centre, Medical University of Vienna, Vienna, Austria, 2Christian Doppler Laboratory for Clinical Molecular MR Imaging, Medical University of Vienna, Vienna, Austria
Synopsis
A density weighted concentrically circular echo-planar trajectories readout scheme is presented for brain MRSI at 7 T. We give an analytic solution for the variable radii distribution in order to intrinsically measure a Hamming weighted k-space. A comparison with post acquisition filtered equidistant concentric circles is done. Invivo metabolic maps and spectra are shown.
Introduction
In contrast to traditional phase encoded chemical shift imaging, spatio-spectrally encoded sampling schemes offer the advantage of a reduced scan time up to two orders of magnitude. At high field strengths of 7T matrix sizes of 64$$$\times$$$64 or higher can be hardly achieved with spirals or EPSI because hardware limitations dramatically decrease the achievable spectral bandwidths. Concentrically circular echo-planar trajectories (CONCEPT$$$^1$$$), however, suffer less from these constraints that much because they are shorter than spirals and selfrewinding. Therefore CONCEPT can achieve high spectral bandwidths while still preserving 100% sampling efficiency and thus higher SNR per time in contrast to spiral and EPSI. The SNR per time can be further increased by combining CONCEPT with density weighted acquisition (DWA). It has already been shown$$$^{2,3,4}$$$ that DWA optimizes the noise variance since no post acquisition filtering is needed. Instead the target filter is achieved by intrinsically weighting k-space due to non-uniformly sampling. We chose the Hamming filter $$$\mathcal{H}(k)$$$ as the target filter in order to optimize the point spread function (PSF) for reduced voxel bleeding (lipid artifacts).Methods
Two different methods were compared: a) DWA with a Hamming filter as target filter and b) Equidistant circles with post acquisition Hamming filtering. Four healthy volunteers were measured using a 32 channel head coil using MUSICAL$$$^5$$$ coil combination on a 7T scanner. The used sequence was a single-slice FID sequence$$$^{6,7}$$$ which applied sine and cosine modulated readout gradients for encoding of the kx/ky-plane. The invivo matrix size was 64$$$\times$$$64 which equals 342 circles for the DWA and 32 for equidistant circles. We measured 512 spectral points which correspond to 512 repetitions for each circle, the spectral bandwidth was 1900Hz with 2 temporal interleaves. The acquisition delay was 1.3ms, the TR 600ms. The acquisition time was 8min20s which corresponds to one average for DWA and 13 averages for equidistant circles. For the reconstruction we used convolution gridding with five times overgridding to minimize polar sampling artifacts. A linear phase correction was applied before gridding to compensate for the different acquisition time points of each sample along each circle. Fitting of the spectra was done with LCModel and metabolic maps were processed.Theory
Assuming continuous polar sampling, the sample density in k-space is given by the absolute value of the Jacobian determinant $$$J^8$$$ of the transformation
$$k_x=K(k)\text{cos}k_{\phi}$$
$$k_y=K(k)\text{sin}k_{\phi},$$
as already hinted in Lauzon et al.$$$^9$$$. The function $$$K(k)$$$ describes the non-uniform radii distribution and has to fulfill the boundary conditions $$$K(k^{max})=k^{max}$$$ and $$$K(0)=0$$$. Setting $$$J=K'K$$$ proportional to the inverse of the (polar) Hamming filter $$$\mathcal{H}(K(k))=\alpha-\beta \text{cos}(\pi K(k)/k_{max})$$$ we obtain
$$K'(k)K(k)=c/\mathcal{H}(K(k)).$$
Solving the above differential equation by separation of variables gives
$$$k(K)=\left(\alpha\frac{K^2}{2}+\beta \frac{k_{max}^2}{\pi^2}\text{cos}(\pi K/k_{max})+\beta\frac{k_{max} K}{\pi}\text{sin}(\pi K/k_{max})-\frac{\beta k_{max}^2}{\pi^2}\right)/\left(k_{max}\left(\frac{\alpha}{2}-\frac{2\beta}{\pi^2}\right)\right),$$$
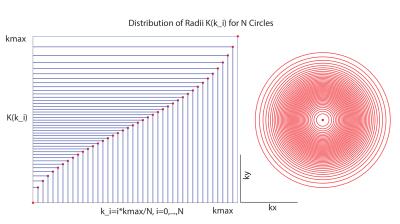
where $$$c$$$ and the constant of integration are determined by the boundary conditions. The inverse of the above function, $$$K(k)$$$, is the function of interest which can not be calculated analytically. However we can approximate $$$K(k)$$$ using inverse series expansion. Evaluation of $$$K$$$ at the discrete coordinates $$$k_i=ik_{max}/N$$$ for $$$i=0,...,N$$$ gives the distribution of the $$$N$$$ Radii in order to sample a Hamming weighted k-space.
Results
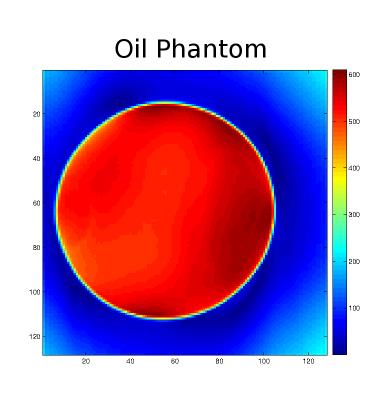
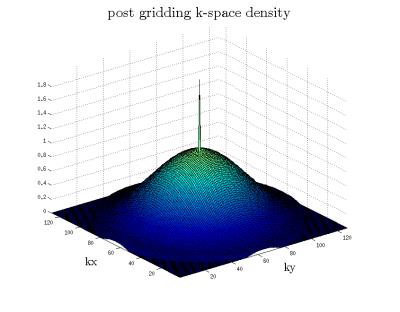
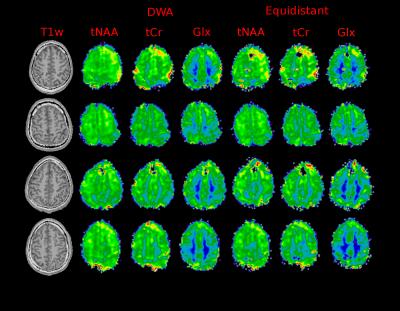
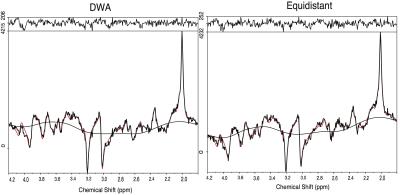
Figure (1) shows the distribution for the radii and the resulting trajectories. Figure (2) shows the localization of an oil phantom using DWA and a matrix size 128$$$\times$$$128 (1405 circles). The smoothing effect of the Hamming weighting can be clearly observed. The achieved k-Space weighting with the DWA is presented in figure (3). Metabolic maps for tNAA, tCr and Glx - for DWA and equidistant circles - are shown in figure (4) together with T1w images. DWA results in an increase of the median SNR of 18.2%, 7.7%, 16.7% and 23.1% for the four volunteers. Figure (5) shows selected spectra for DWA and equidistant circles of the second volunteer.Discussion
We showed that the SNR per time gain caused due to DWA improves the quality of the metabolic maps in contrast to post acquisition filtering. It was also shown that measuring high matrix sizes is feasible at 7T in an acceptable acquisition time with optimal SNR per time. Both techniques result in the same PSFs, however pre gridding the weighting of k-Space can be smoother approximated with DWA because DWA allows for denser sampling. DWA for CONCEPT requires few additional trajectories in contrast to other sequences because the density of equidistant CONCEPT is already close to a Hamming filter due to $$$J=1/k$$$ (since $$$K(k)=k$$$) which results in a stronger weighting of the origin. The holes in some metabolic maps are caused by baseline artifacts which may arise from imperfect density compensations.Acknowledgements
The authors want to thank Borjan Gagoski for helpful discussions.
This project was funded by the Austrian FFG: #FA771E0801.
References
1. Furuyama et al, MRM 67, 2012.
2. Kasper et al, NeuroImage 100, 2014.
3. Pohman et al, MRM 45, 2001.
4. Mareci et al, Journal of MR 92, 1991.
5. Strasser et al, NMR Biomed. 26, 2013.
6. Bogner et al, NMR Biomed 25, 2012.
7. Henning et al, NMR Biomed 22, 2009.
8. Hoge et al, MRM 38, 1997.
9. Lauzon et al, MRM 40,1998.
Figures