Synopsis

This work presents a novel method for macromolecule mapping and quantification. The proposed method integrates an FID-based MRSI acquisition with a generalized series (GS) model based extrapolation scheme. The FID acquisition allows for the use of ultrashort echoes and short repetition times for fast imaging with improved SNR efficiency. The GS model effectively makes use of the spectral priors from single voxel spectroscopy and allows for reformulating the back-extrapolation of metabolite signals as a linear problem (in contrast to conventional nonlinear methods). Results from in vivo experiments demonstrate that MM signals estimated by the proposed method are consistent with an inversion recovery based method and lead to better metabolite quantification.

Introduction

Theory

Signal model

The proposed method represents the MRSI signals $$$s\left(\mathbf{r},f\right)$$$ using the following GS-based model

\begin{eqnarray*} s\left(\mathbf{r},f\right) & = & \sum_{p=1}^{P}g_{p}(\mathbf{r})\phi_{p}(f)+s_{MM}\left(\mathbf{r},f\right)\\ & = & \sum_{p=1}^{P}g_{p}(\mathbf{r})s_{ref}(f)e^{-i2\pi fp\Delta t}+s_{MM}\left(\mathbf{r},f\right). \quad\quad [1]\end{eqnarray*}

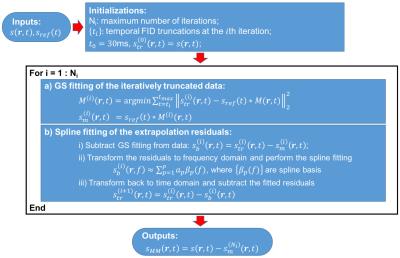
$$$\left\{\phi_{p}(f)\right\}$$$ are the GS bases constructed under maximum cross entropy principle with a metabolite reference $$$s_{ref}(f)$$$⁶ and $$$\left\{g_{p}(\mathbf{r})\right\}$$$ the corresponding coefficients. $$$s_{MM}\left(\mathbf{r},f\right)$$$ represents the MM component. The use of GS model is motivated by its representation efficiency and success in data extrapolation provided a good reference⁶. This is very desirable for MRSI since high-quality spectral priors can be obtained from SVS experiments. Given $$$s_{ref}(f)$$$ and the model in Eq. [1], we developed an iterative FID-truncation and back-extrapolation algorithm to remove the metabolite component from $$$ s\left(\mathbf{r},f\right)$$$ and extract $$$s_{MM}\left(\mathbf{r},f\right)$$$. This algorithm is described Fig. 1.

Estimation of $$$s_{ref}(f)$$$/$$$s_{ref}(t)$$$

To construct a good reference, $$$s_{ref}(f)$$$, we acquire a set of high-SNR SVS data and perform the following spectral fitting

\begin{eqnarray*}\hat{T}_{2,m},\hat{a}_{m,TE_{i}},\delta f & = & \sum_{TE_{i}=1}^{I}\sum_{n=1}^{N}\left|s_{TE_{i}}(t_{n})-env(t_{n})\sum_{m=1}^{M}a_{m,TE_{i}}e^{-t_{n}/T_{2,m}}\phi_{m,TE_{i}}\left(t_{n}\right)e^{-i2\pi\delta ft_{n}}\right|_{2}^{2},\\\end{eqnarray*}

where $$$s_{TE_i}$$$ denotes the SVS data with different TEs. $$$\phi_{m,TE_i}$$$, $$$T_{2,m}$$$, $$$a_{m,TE_i}$$$ denote the basis functions, relaxation parameters and relative concentrations for different metabolites. $$$\delta f$$$ accounts for a global frequency discrepancy and $$$env(t)$$$ denotes an envelope function. Using more than one TEs further exploits the J-coupling differences between MMs and metabolites thus improves their separation². $$$s_{ref}(t)$$$ is then synthesized as $$$s_{ref}(t)=\sum_{m=1}^{M}\hat{a}_{m,TE_1}e^{-t/\hat{T}_{2,m}}\phi_{m,TE_1}\left(t\right)$$$ and fed into the proposed algorithm.

Results

In vivo data were acquired on a Siemens Trio 3T system to evaluate the proposed method. To this end, an FID-CSI sequence with ultrashort-TE, short-TR and IR capabilities was developed. The SVS data were acquired at two TEs (30 and 100ms, 2s TR, WET water suppression, PRESS localization) and water FIDs were acquired for estimating $$$env(t)$$$ (32 TEs, 30ms-340ms, 1min). MPRAGE images and B₀ field maps were acquired to provide the information for nuisance removal⁷ and B₀ inhomogeneity correction⁸ for the CSI data.

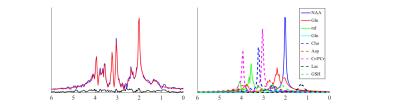
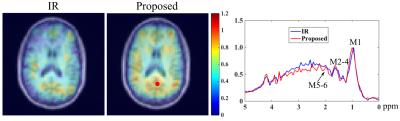
Figure 2 illustrates the spectral fitting results from a set of representative SVS data. A low residual level and good separation of different metabolite components can be obtained, which was used to synthesize $$$s_{ref}$$$. The MM distribution and a representative spectrum obtained by the proposed method from an FID-CSI dataset (TR/TE=800/4ms, 36x36 matrix size, elliptical sampling) are shown in Fig. 3, with comparison to the results from an IR acquisition (TI=600ms, same resolution and TR/TE). Consistent results can be observed.

To demonstrate the utility of the measured MM signals, a set of MM bases $$$\left\{v_{l}(t)\right\}$$$ were estimated from $$$s_{MM}\left(\mathbf{r},t\right)$$$ (by SVD analysis) and incorporated into the following model to quantify the CSI data:

\begin{eqnarray*}s(\mathbf{r},t) & = & \sum_{m=1}^{M}c_{m}(\mathbf{r})e^{-t/T_{2,m}^{*}(\mathbf{r})+i2\pi\delta f_m(\mathbf{r})t}\phi_{m}(t)+\sum_{l=1}^{L}b_{l}(\mathbf{r})v_{l}(t)\\\end{eqnarray*}

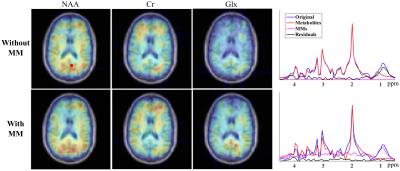
where $$$\left\{b_{l}(.)\right\}$$$ denotes the spatially-dependent coefficients and $$$\delta f_m(\mathbf{r})$$$ accounts for residual frequency discrepancy. Figure 4 compares the quantified metabolite maps with and without $$$\left\{v_l(t)\right\}$$$. As can be seen, incorporating MM bases leads to higher-quality metabolite maps with less spatial variation. We note that the 800ms TR, chosen to match the IR acquisition, can be shortened significantly for the proposed method. MM maps and spectra from different subjects are shown in Fig. 5.

Conclusion

Acknowledgements

References

[1] Behar KL, Rothman DL, Spencer DD, and Petroff OA, Analysis of macromolecule resonances in 1H NMR spectra of human brain. Magn. Reson. Med., 1994;32:294-302.

[2] Cudalbu C, Mlynarik V, and Gruetter R, Handling macromolecule signals in the quantification of the neurochemical profile. J. Alzheimers Dis., 2012;31:S101-115.

[3] Povazan M, Hangel G, Strasser B, Gruber S, Chmelik M, Trattnig S, and Bogner W, Mapping of brain macromolecules and their use for spectral processing of 1H-MRSI data with an ultra-short acquisition delay at 7T. NeuroImage, 2015;121:126-135.

[4] Seeger U, Klose U, Mader I, Grodd W, and Nagele T, Parameterized evaluation of macromolecules and lipids in proton MR spectroscopy of brain diseases. Magn. Reson. Med., 2003;49:19-28.

[5] Ratiney H, Coenradie Y, Cavassila S, van Ormondt D, and Graveron-Demilly D, Time-domain quantitation of 1H short echo-time signals: Background accommodation. Magn. Reson. Mater. Phys. Biol. Med., 2004;16:284-296.

[6] Liang ZP and Lauterbur PC, An efficient method for dynamic magnetic resonance imaging. IEEE Trans. Med. Imag., 1994;13:677-686.

[7] Ma C, Lam F, Johnson CL, and Liang ZP, Removal of nuisance signals from limited and sparse 1H MRSI data using a union-of-subspaces model. Magn. Reson. Med., 2016;75:488-497.