Introduction

Spatially-selected RF pulses lead to spatial dependence of spin magnetization evolution. Consequently, numerical simulations of three-dimensionally localized magnetic resonance spectroscopy (MRS) are time-consuming for multiple spin systems because of the need to compute an ensemble of spins in three dimensional space. In many cases either ideal RF pulses or reduced spin density matrices are used for simulations. As numerical simulation gains increasing popularity for designing and validating in vivo MRS detection methods as well as for providing quantification basis sets [1-3], improving the efficiency and accuracy of spin density matrix simulation is much needed. This abstract reports a highly accelerated and accurate method for simulating spatially localized MRS spectra.

Methods

The time evolution of spatially localized multispin density matrix as the full solution to the Liouville–von Neumann equation was analyzed. It was found that spatial coordinates of the full set of spin density operators labeled by slice selection gradients can be projected onto one dimension after slice selection as long as the crusher gradients are refocused. Therefore, the conventional three-dimensional simulation can be converted to a one-dimensional problem in cases such as the commonly used PRESS or STEAM. The proposed method was implemented using a computer program written in Java language. It was validated by comparing with the conventional GAMMA [4] simulation and with phantom experiments. The time evolution of spatially localized multispin density matrix as the full solution to the Liouville–von Neumann equation was analyzed. The spatial coordinates of the full set of spin density operators labeled by slice selection gradients were projected onto one dimension after slice selection. The proposed method was implemented using a computer program written in Java language. It was validated by comparison with the conventional GAMMA [4] simulations and with phantom experiments. Furthermore, the simulated spectra were used as basis set (18 metabolites) to fit in vivo short echo time spectra acquired from human brain at 3 T.

Results

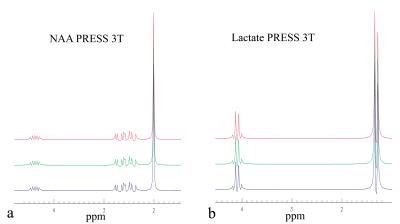
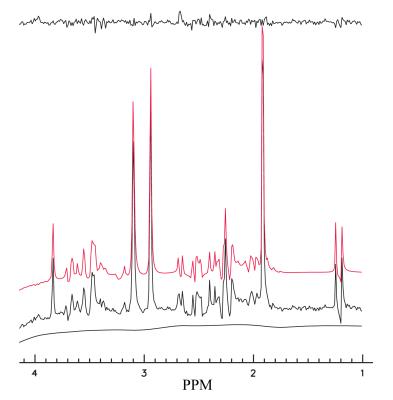
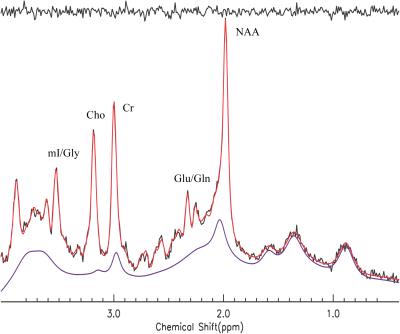
Figure 1 shows the comparisons between three different simulations of PRESS-localized NAA and Lac spectra at 3 T; the simulation (red spectra) using GAMMA C++ library and three-dimension computation, the simulation (green) using GAMMA C++ library and the proposed one-dimensional projection method, and the simulation (black) using the Java-developed program in this study and the proposed one-dimensional projection. The voxel was represented by 100 × 100 × 100 equally spaced points. As seen in Figure 1, they are completely identical. All computations were performed on PC. The two simulations with the one-dimensional projection method used 10 seconds or less for NAA (acetyl moiety and aspartate moiety were combined) and Lac; in contrast, the conventional three-dimensional computation took over 16 hours. Figure 2 shows the fit of short TE phantom spectrum (black color) using the simulated basis sets (red color). The estimated metabolite concentrations (relative to creatine) was in good agreement with those of the listed ingredients of the phantom ( ±4%) which consisted of NAA (12.5mM), creatine (10 mM), glutamate (12.5 mM), myo inositol (7.5mM), and lactate (5 mM). The baseline was originated from the residual water after water suppression. Figure 3 shows an example of using the one dimensional projection method to simulate basis sets (red) for fitting an in vivo short TE spectrum (black) . The estimated metabolite concentrations (mM ± standard deviation (SD)) averaged over twelve healthy subjects were: [tNAA] = 13.6 ± 4.9% , [tCr]= 9.5 ± 5.8%, [tCho] = 2.4 ± 10.1%, [Glu] = 11. 8 ± 6.7%, [Glx] = 14.3 ± 9.4%, [mI] + [Glycine] = 8.99 ± 7.7%, [mI] = 6.78 ± 12.5%, and [Glutathione] = 1.48 ± 23%.

Discusssion

The new method represents a dramatic improvement in efficiency and accuracy for the simulation of spatially localized MRS. Thanks to the massive increase in computational efficiency, more spatial points can now be used to define the three dimensional voxel, leading to more realistic simulation. To the best of our knowledge, the current work was the first to show full spin density simulation with spatial points exceeding 100 in each of the three dimensions. Using the one-dimensional projection method the computation time was as short as ~10 minutes with a typical desktop computer for a six spin molecule.The resultant simulation agreed well with the phantom experiment as demonstrated by Fig. 2. As simulation time of the one-dimensional projection method is mainly consumed by computing the propagators which are prepared prior to computing the spin density evolutions, simulating a 2D or higher dimensional spectrum such as J-resolved spectrum can be made very efficient―the preprepared propagators can be repeatedly called back throughout the 2D or higher dimensional loop―and can be accomplished in a time frame similar to the case of a 1D spectrum.

Conclusion

The dramatically enhanced computational efficiency makes spin density matrix simulation of multi-spin systems a convenient tool for designing and optimizing MRS pulse sequences and for computing basis sets for spectral fitting. As many experiments such as two-dimensional spectroscopy and T2 measurements demand highly extensive simulation the proposed method is expected to greatly facilitate progress in those areas.

Acknowledgements

No acknowledgement found.