Introduction

Spinal cord stimulation (SCS) is an established therapy for treatment of chronic pain of the back and limbs. The SCS lead is placed in the dorsal epidural space and is connected to an implanted pulse generator (IPG) placed in a subcutaneous location that delivers electrical current through the lead to the spinal cord. RF-induced heating during an MRI scan can pose a risk to patients implanted with a SCS device. The amount of RF-induced lead heating is mainly attributed to the electric field tangential (Etan) to the lead path, which can be predicted by using an electrical field transfer function (TF) associated in different media. The ISO/TS 10974 RF heating methodology states that both HPM and LPM should be evaluated for SCS systems since more than 10% of the lead length are tunneled subcutaneously. The objective of this study is to compare electric field transfer functions (TFs) of a SCS system in high permittivity media (HPM), low permittivity media (LPM) and in mixed media spinal cord (SC) by using computer simulations.

Methods

The ANSYS HFSS software package was used to calculate the electromagnetic field distribution in a model built from the TF measurement set-up. A St. Jude Medical Orion IPG and a percutaneous Octrode lead model with lead length of 60 cm was built inside a tank (120 cm by 15 cm by 10 cm). The tank is filled with homogenous media such as global average (HPM) (σ=0.47 S/m; ε =78) from ASTM F2182 or fat tissue (LPM) (σ=0.0531 S/m; ε =11.5) from ISO/TS 10974. For the mixed media of SC, we modeled the anatomical and conductive properties of the lower thoracic (T7-T10) spinal cord. Additionally, the lead was placed symmetrically over the spinal cord cerebrospinal fluid (CSF) layer (σ=2.066 S/m; ε =97.3) within the dorsal epidural space (σ= 0.04 S/m, ε =6.5) with lead position varied dorsally. The lumens of the lead were filled with either air (dry) or fluid (wet). The reciprocal method was used with current excitation was at the distal electrode. Currents along lead conductors are obtained by loop integrals of H fields at 1 cm increments starting from the distal electrode. The TFs are the currents along the lead divided by the excitation, denoted as S(τ). The RF heating can be estimated¹ by using ΔT = |ΣEtan(τ) *S(τ) dτ | and the theoretical worst case is ΔT = A|Σ |Etan(τ)| *|S(τ)| d t |2 when Etan is conjugate of S, where A is a coefficient.

Results

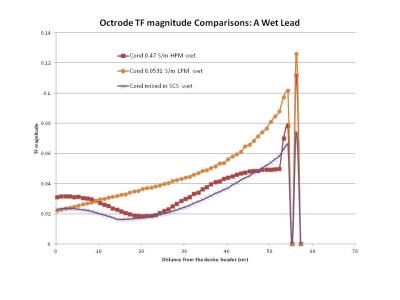
The curves of TF magnitudes |S(τ)| for HPM and mixed in SCS follow each other closely, while the TF shape and scaling in LPM is significantly different. The case with a wet lead is shown in Figure 1.

Conclusions

The results indicate that SCS TF measurement and validation should be performed in HPM since it has the closest match with mixed media SC. With the SC mixed media model, the compound tissue effect from epidural fat and CSF around the lead was seen and the TF follows that of the HPM TFs closely. Lowering HCM conductivity would shift the curve slightly above that with the SC model for in-vivo in order to ensure a worse case. This can be further validated through DT calculation of TF equation by integrals of Etan along clinical SCS implant pathways for in-vivo temperature distribution estimation.

Acknowledgements

No acknowledgement found.

References

1: Park SM, Kamondetdacha R, Nyenhuis JA. Calculation of MRI-induced heating of an implanted medical lead wire with an electric field transfer function. J Magn Reson Imaging. 2007 Nov;26(5):1278-85.