5461
Analytic Validation of a Computational Model of Magnetic Force in Linear Magnetic Materials1Medical Biophysics, Western University, London, ON, Canada, 2Physics and Astronomy, Western University, London, ON, Canada
Synopsis
The current procedures and guidelines for testing forces on medical devices require that testing be performed in a MR setting, which is both timely and costly. To reduce test time and cost, a computational model of magnetic force was developed. Using a test case where an analytic solution of magnetic force can be applied, it is shown that for materials with magnetic susceptibility (chi)<105 ppm, a computational model of magnetic force was correct within 10% error and this error decreases to less than 1% for chi<104 ppm. Size of object is shown to have little effect on error.
PURPOSE
Materials with a non-zero magnetic susceptibility will always experience a force in the presence of strong spatially varying magnetic fields, such as those present in MRI. The magnetic forces experienced by medical devices in the MR environment are often unknown and can present a danger to the subject, and/or interfere with the normal operation of the MR scanner.1 The current procedures and guidelines for testing medical devices require that testing be performed in a MR setting, which is both timely and costly.2 To reduce test time and cost, a computational model of magnetic force was developed. Using a test case where an analytic solution of magnetic force can be applied, this work seeks to compare and validate the in-silico results of magnetic force.METHODS
A background magnetic flux density with spatial gradient <-0.5, 0, 0.5> was implemented at all boundaries of a cubic simulation domain using COMSOL (version 5.2a). Within this domain a cylinder of radius 1.27cm, length L and magnetic susceptibility chi was placed along the z axis, with the center of the base of the cylinder at isocentre. This positioning allowed sufficient symmetry such that Fx,Fy=0, simplifying the analytic solution.
Results of magnetic force were produced for two simulation sets. First, the length of the cylinder was kept constant at 2.54cm and simulations were run varying the magnetic susceptibility of the cylinder from 1 to 106 ppm. Next, the magnetic susceptibility was kept constant at 100ppm and simulations were run varying the length of the cylinder from 1.27 to 25.4 cm.
Magnetic flux density, magnetization, mesh element volume, and spatial gradient of the B field data - all as a function of position - was exported from the simulations and used to calculate the magnetic force in Matlab (version 2015b). This calculation was performed with equation (1) of figure 1, using the simulation data as an input.
In order to validate the results of the simulations, an analytic model of magnetic force was produced, equation (2) figure 1, and this model was solved for all cases between simulation sets.
RESULTS
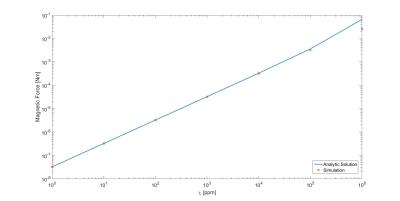
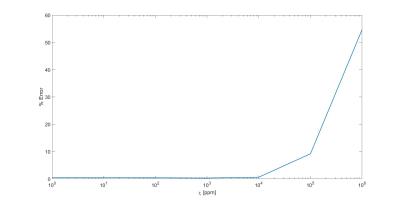
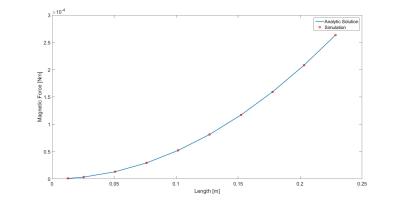
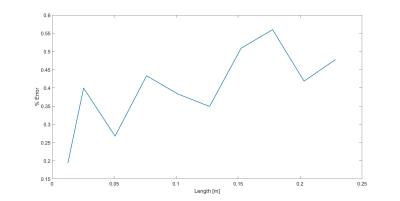
The results from varying the magnetic susceptibility of the cylinder with a constant length are shown in figure 2 with associated in error displayed in figure 3. Results from varying the length of the cylinder at a constant magnetic susceptibility are shown in figure 4 with associated in error displayed in figure 5.DISCUSSION
Figure 2 shows a linear increase in both simulated and analytic magnetic force for values of magnetic susceptibility below 105 ppm. For larger susceptibilities the simulation begins to underestimate force. Figure 3 shows the percent error between the two data sets. Error is less than 1% for chi<104 ppm, and less than 10% for chi<105 ppm. The increase in error is most likely due to the inability for the simulation to compensate for the increasing effect the magnetization has on the surrounding field as chi increases. Implant-grade metals (ie. stainless steel 316, cobalt-chromium alloys, titanium alloys) all have chi less than or on the order of 104 ppm, where error would be less than 1%.
Figure 4 shows both the analytic and simulated force due a cylinder of varying length. The percent error between the two data sets, shown in figure 5, increases slightly as length increases but is less than 0.6% for all lengths.
CONCLUSION
It was shown that for materials with magnetic susceptibility <105 ppm, a computational model of magnetic force was correct within 10% error and this error decreases to less than 1% for chi<104 ppm. Size of object was shown to have little effect on error. The computational model of magnetic force is sufficient to predict magnetic forces on materials with magnetic susceptibility less than 105 ppm, and is ideal for use on materials with magnetic susceptibility less than 104 ppm such as implant-grade metals.Acknowledgements
I would like to acknowledge the members of the Chronik lab at Western University for their helpful discussions concerning the formatting of the figures in this abstract.References
1. Shellock, F. G., Woods, T. O., & Crues, J. V. (2009). MR Labeling Information for Implants and Devices: Explanation of Terminology. Radiology, 253(1), 26–30. https://doi.org/10.1148/radiol.2531091030
2. ASTM F2052-14: Standard Test Method for Measurement of Magnetically Induced Displacement Force on Medical Devices in the Magnetic Resonance. Pennsylvania, USA; ASTM International, 2014.
Figures