Introduction

Due to the complexity of assessing RF-induced heating in-vivo, computational modeling has been widely used. To assess RF-induced heating of conductive elongated devices (e.g., leads of medical devices), it is necessary to know the incident tangential electric field (E_tan) along the device trajectory. The electric (E) and magnetic (H) fields induced in a patient, or a phantom, depends on the coil geometry (i.e., coil length and diameter, rungs), the electrical circuitry of the feeds, coil excitation, and coil losses. Numerical simulations are often used to compute the E_tan, because the measurement of E field is challenging. The effect of coil losses on E and H are often neglected in literature. We herein show the dependence of E and E_tan generated in the ASTM phantom¹ on the coil losses.

Method

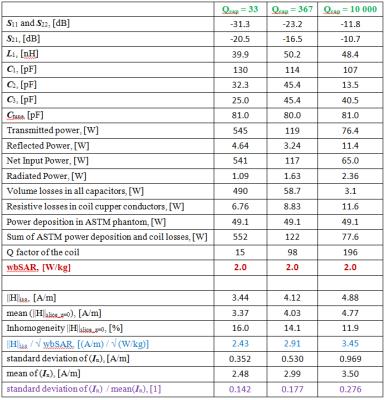
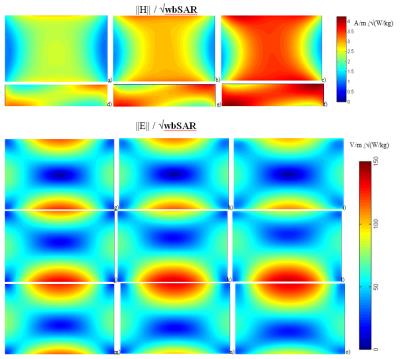
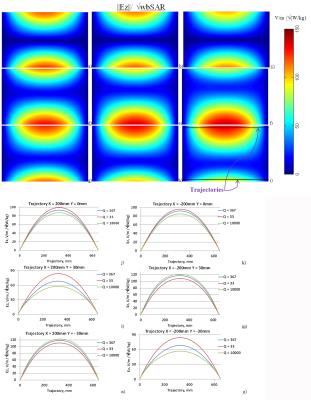
The simulated coil was a 64 MHz 16-rung high pass birdcage body coil (Fig. 1a) based with the dimensions of the Medical Implant Test System (Zurich Med Tech, Switzerland) . Coil losses were modified by applying three different capacitor Q factors (Q_cap): 33 (previously used in²), 367 (to mimic a low-quality capacitor), and 10000 (to model nearly lossless capacitors). The RF feed sub-circuit providing impedance matching and decoupling of the two channels was the multi-element circuit shown in Fig. 1b (see³ for additional details). The coil was tuned for the three Q_cap cases (Fig. 1c) and driven in quadrature mode. 3D EM simulations were performed with HFSS (ANSYS, Canonsburg, PA, USA). The mesh adaptation procedure with 30% increase of mesh elements was stopped if the variation of ||E||max (maximum of electric field magnitude (||E||) over entire ASTM phantom) between two consecutive meshes was less than 3%. E and H inside the ASTM phantom were obtained on an equidistant mesh of 1 mm. ||E|| and the magnitudes of the z and x components (i.e., ||E_z|| and ||E_x||) were analyzed on three coronal planes (i.e., y={-30,0,30} mm). The values of E and H, as well as the current magnitudes in each rung (I_n, n=1 to 16) were normalized to obtain a whole-body average SAR (wbSAR) in the ASTM phantom of 2 W/kg.

Results and Discussion

Decreasing Q_cap resulted in decreasing of both ||H|| at the coil iso-center (||H||_iso), and ||H|| averaged over the axial slice at z=0 (||H||_{slice_z=0}). For Q_cap=10000, I_n were mostly defined by the distance between the given rung and the ASTM phantom. The variation of I_n expressed as the ratio of the I_n standard deviation to the I_n mean value was twice as much for Q_cap=10000 than for Q_cap=33. For Q_cap=10000, the resistive losses of the coil, due to the presence of the copper material, were 15% of the transmitted power and 25% of the power deposited in the ASTM phantom. Numerical errors caused a discrepancy between the transmitted power and the sum of power depositions and coil losses of less than 2% (Table 1). Change of Q_cap resulted in substantial changes of E across the ASTM phantom (Fig.2 g-o). Additionally, there were visible variations of ||E_z|| up to 100% along a line at x=200mm and y=30mm, which is a typical location to place implants for heating testing¹ (Fig. 3j-o). Our results indicate that the use of E/||H||_iso or E/||H||_{slice_z=0} normalization to predict E inside a human body located in a commercial birdcage coil based on a numerical coil model with arbitrary coil losses can result in high errors. The ratios of ||H||_iso/√wbSAR or ||H||_{slice_z=0}/√wbSAR are unknown for commercial coils and can vary significantly due to using different coil components. For a given ||H||_{slice_z=0}, the discrepancy of ||H||_{slice_z=0}/√wbSAR between the numerical coil model and the physical coil can lead to erroneous prediction of wbSAR. Because the wbSAR is defined by E distribution in the human body, a wrong prediction of wbSAR would generate a wrong prediction of E, with a related possible incorrect RF exposure assessment.

Conclusion

The results of this study showed that H/√wbSAR depends on Q_cap. To avoid systematic errors in predicting E inside a human body the coil model should include realistic coil losses. To model a physical coil with unknown coil losses one can iteratively adjust the coil losses followed by experimental verification. The dependence of the ratio ||H||_iso/√wbSAR on Q_cap in this study cannot be readily generalized to the wider range of birdcage coil because only one coil geometry was herein investigated.

Disclaimer

The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or suggested endorsement of such products by the Department of Health and Human Services.

Acknowledgements

No acknowledgement found.