Synopsis

We propose a method for correcting gradient artefacts in simultaneous EEG-FMRI that are variable from shot-to-shot, where artefacts cannot be identified via averaging. The artefact model is extracted from a data-driven decomposition that identifies the signal contributions which show geometric variation matching that of the trajectory rotation model. We show that this correction, applied to a rotating EPI trajectory, works just as well as standard approaches applied to conventionally sampled (non-rotating) EPI data. This will allow the use of more flexible sampling approaches in simultaneous EEG/FMRI that facilitate highly accelerated dynamic image reconstruction.

Introduction

We demonstrate a correction method for EEG gradient artefacts during simultaneous EEG-FMRI recording when the gradient waveforms are unique from shot-to-shot, and thus not suitable for correction by artefact averaging across measurements.

Commonly, simultaneous EEG-FMRI data are acquired using EPI, where the gradient-induced artefacts are identical from shot-to-shot, and an artefact model can be built up using the Average Artefact Subtraction (AAS) method¹. However, many accelerated imaging methods developed to meet demand for increasing spatial/temporal resolution require time-varying trajectories, including any multi-shot techniques^2,3 as well as compressed sensing⁴ or low-rank methods⁵ that exploit the time domain for reconstruction. One consequence of time-varying trajectories is that the gradient waveforms are not identical from shot-to-shot, and may never repeat, and therefore cannot be subject to averaging.

We propose a data-driven artefact model which extends the optimal basis set modelling approach⁶ by including the expected geometric variation in input gradient waveforms that are arbitrarily rotated. We show that this approach is capable of removing artefacts at least as well as the AAS method does in conventionally sampled data.

Methods

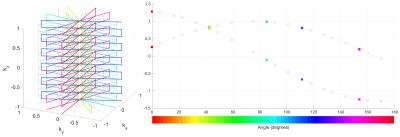
The proposed method requires a simple model of the gradient-induced flux projected onto an axis defined by the effective loop of an EEG electrode. In rotation of the gradient waveforms about a single fixed axis, the geometric projection model is $$$A sin(\theta+\phi)+c$$$, where $$$\theta$$$ is the trajectory rotation angle, and $$$(A,\phi,c)$$$ are fitted parameters capturing the rotation-dependent flux changes. These parameters depend on the physical position and orientation of the EEG channel leads⁷ (Fig. 1), and thus need to be estimated for each channel independently.

The correction procedure is as follows (for each channel):

1. Detrend and reshape the EEG time-course into a matrix $$$D$$$ of size $$$T\times N$$$, where $$$T$$$ is the number of EEG samples per MRI measurement, and $$$N$$$ is the number of measurements used to define the artefact model

2. Perform a singular value decomposition of $$$D$$$, to produce $$$D=USV^{'}$$$, where $$$U$$$ contains artefact waveforms, and $$$V$$$ characterises the rotational variation

3. For each column $$$v$$$ in the right singular vectors $$$V$$$, fit the model $$$A sin(\theta+\phi)+c$$$ to the coefficients of $$$v$$$

4. Identify the set of components $$${i}$$$ that significantly fit the model (e.g. by using a $$$\chi^{2}$$$ goodness-of-fit test ) up to some chosen number of components

5. Construct the artefact model, $$$M=U_{{i}}S_{{i}}V_{{i}}^{'}$$$ , where the corrected data is then computed as $$$D_{corr}=D-M$$$

Here, we demonstrate the proposed correction using a radial-Cartesian trajectory (TURBINE⁸) that rotates EPI-readouts from shot-to-shot about the phase encoding (z) axis by the golden angle with a small random perturbation to sweep out a cylindrical k-space. EEG data were collected using a 32-channel MRI compatible EEG system at 3 T in two subjects. Conventional EPI acquisition data were also acquired and pre-processed using the vendor supplied AAS implementation for comparison.

Results

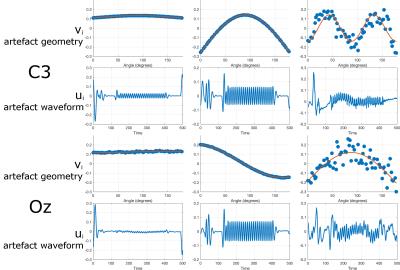
Fig. 2 shows estimated artefact components for two different EEG channels in a representative subject. The identified right singular vectors significantly fit the trajectory model, and typically > 99.99% of the signal variance is captured in the first two components. Differences in the amplitude and phase model parameters can be seen across channels, reflecting their different physical geometries. Interestingly, harmonics of the form $$$A_{n} sin(n\theta+\phi_{n})+c_{n}$$$ where $$$n=1,2,3...$$$ were also found to capture gradient-related variance.

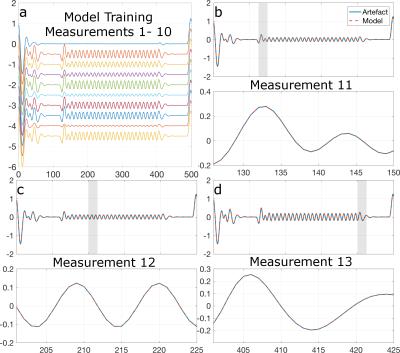
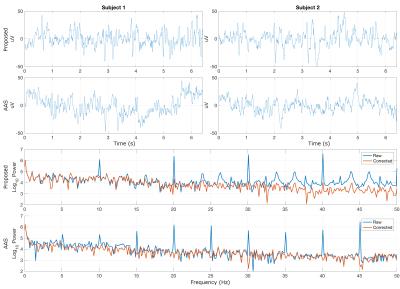
Fig. 3 shows, for demonstration purposes, an artefact model derived from 10 TURBINE measurements with distinct artefact signatures (Fig. 3a), used to predict the artefact response for unseen TURBINE measurements based on their known trajectories (Fig. 3b-d). Figs. 4a-b show corrected time courses for a single representative channel using the proposed method on TURBINE data showing no apparent gradient contamination. For comparison, Figs. 4c-d show corrected recordings in the same channels during an EPI acquisition in the same session using AAS correction. Figs. 4e-f show log spectral power for the data from subject 1, highlighting the reduction in artefact power (spikes) using both the proposed method (TURBINE data) and AAS (EPI data).

Discussion

Acknowledgements

References

1. Allen, P. J., Josephs, O., & Turner, R. (2000). A method for removing imaging artifact from continuous EEG recorded during functional MRI. NeuroImage, 12(2), 230–239.

2. Lee, G. R., Griswold, M. A., & Tkach, J. A. (2010). Rapid 3D radial multi-echo functional magnetic resonance imaging. NeuroImage, 52(4), 1428–1443.

3. Chowdhury M. E. H., Mullinger K. J., Spencer G. S., & Bowtell R. (2015). Removing the gradient artefact caused by 3D EPI in simultaneous EEG-fMRI experiments using a gradient model fit. Proc ISMRM, #3943

4. Zong, X., Lee, J., John Poplawsky, A., Kim, S.-G., & Ye, J. C. (2014). Compressed sensing fMRI using gradient-recalled echo and EPI sequences. NeuroImage, 92C, 312–321.

5. Chiew, M., Graedel, N. N., Mcnab, J. A., Smith, S. M., & Miller, K. L. (2016). Accelerating functional MRI using fixed-rank approximations and radial-cartesian sampling. Magnetic Resonance in Medicine (Online Early View)

6. Niazy, R. K., Beckmann, C. F., Iannetti, G. D., Brady, J. M., & Smith, S. M. (2005). Removal of FMRI environment artifacts from EEG data using optimal basis sets. NeuroImage, 28(3), 720–737

7. Yan, W. X., Mullinger, K. J., Brookes, M. J., & Bowtell, R. (2009). Understanding gradient artefacts in simultaneous EEG/fMRI. NeuroImage, 46(2), 459–471.

8. Graedel, N. N., Mcnab, J. A., Chiew, M., & Miller, K. L. (2016). Motion correction for functional MRI with three-dimensional hybrid radial-Cartesian EPI. Magnetic Resonance in Medicine (Online Early View)