Purpose

DCM estimates effective connectivity[1; 2; 3] by fitting the neuronal model convolved with the hemodynamic response function to the observed fMRI data. Similar to dynamic functional connectivity [4; 5], the temporal variation of effective connectivity i.e. dynamic effective connectivity can be estimated. Knowing the temporal changes of the neuronal model using DCM might allow us inferring the changes in factors underlying functional connectivity, which we observe by correlating the time series extracted from different regions in the brain [6]. Effective connectivity estimates the interaction between the regions at the neuronal level. However traditionally, DCMs have only been estimated for static case so far. By estimating different DCMs at different time points of the time series, we could potentially model the temporal evolution of effective connectivity. In this study we applied a fully connected DCM model to the resting state fMRI data of mice. The time series data were then splitted in two halves to evaluate the effective connectivity for two time intervals.

Methods

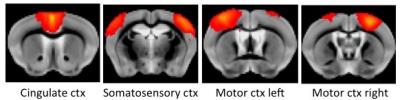
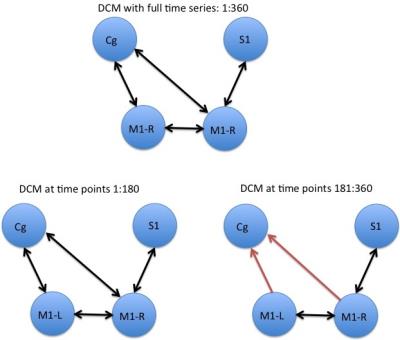
Data acquisition: Resting-state fMRI data sets of anesthetized mice were collected on a Bruker BioSpec 94/30 system operating at 9.4T using a gradient-echo echo-planar imaging (GE-EPI) sequence with 1s temporal resolution. Isoflurane dose of 1.1% was used in an air/oxygen mixture (4:1). Animals were mechanically ventilated throughout the experiment. Data analysis: After preprocessing and realignment, concat-ICA was applied using the MELODIC toolbox of FSL. These results were used for Dual Regression and Network Modeling [7] of the brain networks using FSLNets. Based on the networks that were found significant, we identified 4 ICA components as shown in Figure 1. These ICs were then fed in to the dynamic causal modeling (DCM) framework in the SPM toolbox. In order to estimate the temporal evolution of effective connectivity networks, we divided the time series of 360s (360 volumes with 1 volume/s) in two blocks (0-180s, 181-360s), and ran DCM framework together with Bayesian Model Selection separately for each half of the time series for all subjects. We then applied a fully connected stochastic DCM [6; 8] to the resting state fMRI data, and compared it against a partially connected model. Connection strengths were identified by inspecting the parameter estimates and posterior expectations as stored in DCM.Ep.

Result

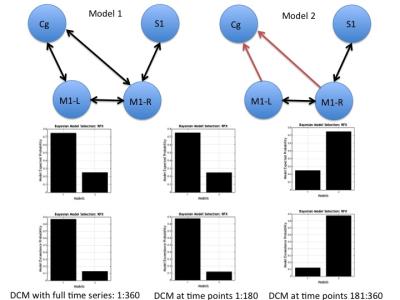
We estimated temporal variations of DCMs by estimating effective connectivity at different time points. Figure 2 shows the final models selected under normal procedure (using full time series length) as well as during estimating the temporal evolution of DCMs. The changes in the estimated model parameters reflect the change in dynamic effective connectivity over time. The results show differences in models because of changes in posterior expectations as calculated by DCM.Ep. In this case, the DCMs estimated from time point 181-360 seconds had a lower excitatory influence from cingulate cortex (Cg) to motor cortex (M) as it was calculated through a two sample t-test with p < 0.05. The final connection strengths were then put into a DCM model and Bayesian Model Selection (BMS) was used to verify the finally selected model. Figure 3 shows the results from BMS.

Conclusion

Time varying DCMs may allow us to capture the effect of transient network patterns under different brain states. In comparison to dynamic functional connectivity analysis, dynamic effective connectivity yields information on the directionality of connections within the network. Dynamic DCMs, as shown in this work, may help identifying group differences based on the estimated time-varying neuronal networks.

Acknowledgements

No acknowledgement found.

References

[1] K.J. Friston, B. Li, J. Daunizeau, and K.E. Stephan, Network discovery with DCM. Neuroimage 56 (2011) 1202-21. [2] J. Kahan, and T. Foltynie, Understanding DCM: ten simple rules for the clinician. Neuroimage 83 (2013) 542-9. [3] K.E. Stephan, W.D. Penny, R.J. Moran, H.E. den Ouden, J. Daunizeau, and K.J. Friston, Ten simple rules for dynamic causal modeling. Neuroimage 49 (2010) 3099-109. [4] X. Di, and B.B. Biswal, Dynamic brain functional connectivity modulated by resting-state networks. Brain Struct Funct 220 (2015) 37-46. [5] A.A. Ioannides, Dynamic functional connectivity. Curr Opin Neurobiol 17 (2007) 161-70. [6] A. Razi, J. Kahan, G. Rees, and K.J. Friston, Construct validation of a DCM for resting state fMRI. Neuroimage 106 (2015) 1-14. [7] S.M. Smith, K.L. Miller, G. Salimi-Khorshidi, M. Webster, C.F. Beckmann, T.E. Nichols, J.D. Ramsey, and M.W. Woolrich, Network modelling methods for FMRI. Neuroimage 54 (2011) 875-91. [8] K.J. Friston, J. Kahan, B. Biswal, and A. Razi, A DCM for resting state fMRI. Neuroimage 94 (2014) 396-407.