SYNOPSIS

Current approaches separately analyze concurrently acquired diffusion tensor imaging (DTI) and functional magnetic resonance imaging (fMRI) data. The primary limitation of these approaches is not to use all available information in estimation of resting state functional connectivity (FC). To overcome this limitation, we developed a Bayesian hierarchical spatio-temporal model that incorporated structural connectivity (SC) into estimating FC, where SC based on DTI was used to construct a prior for FC based on resting state fMRI (rs-fMRI) data. Simulations and data analysis concluded that our model achieved smaller false positive rates and was robust to data decimation compared to the conventional approach.

PURPOSE

The purpose of this study is to propose a Bayesian hierarchical spatio-temporal model with double fusion to incorporate SC information into estimating FC. This approach enables us to fully use available information, which cannot be achieved by the conventional approach that separately analyzes the DTI and fMRI data acquired in the same session.

METHODS

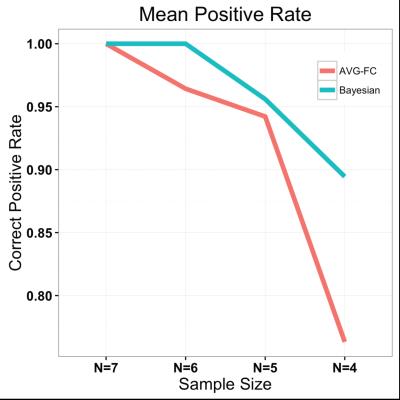
Spatially and temporally correlated resting state fMRI data (T = 128 scans, 100 voxels/ROI, and 5 ROIs) were simulated using autoregressive model with order one (AR(1)) and spatial smoothing approach. Four different spatial smoothing kernels were applied to investigate the effect of the strength of underlying spatial correlation within an ROI on FC estimation, i.e., FWHM = 0, 3.5, 8.2, and . The experimental data were acquired using a Philips Achieva 3T MRI canner equipped with a 32-channel head coil from 7 healthy subjects (37.316.5 years old, two men, right-handed) with no history of neurological and medical conditions. The imaging protocol for each subject included a three-dimensional, T1-weighted high-resolution image series across the whole brain for inter-subject normalization (1 x 1 x 1 mm3) and an fMRI T2* weighted gradient echo, echo-planar image series at rest with eyes closed – matrix 80 x 80, FOV = 240 mm, 34 axial slices, TE = 35 ms, TR = 2 sec, slice thickness = 3.5 mm with 0.5 mm gap, 300 volumes. Diffusion weighted images were acquired to quantify white matter integrity parameters using a single shot, spin-echo, echo-planar sequence - b=1600 s/mm2, 92 diffusion sensitizing directions, TR=8.5 s, TE=65 ms, matrix = 96x96, 50 slices, 2.5 x. 2.5 x 2.5 mm3, no gap, 3 averages. The experimental data consisted of T=300 scans, 8 ROIs (Table 1), and 300 voxels/ROI. Once SC and naïve FC were estimated via the probabilistic tractography¹ and computing the correlation between a pair of ROI-level time series, respectively, the Cholesky decomposition was employed into the SC and naïve FC to generate a lower triangular matrix corresponding to each connectivity matrix. Then a linear combination of these two lower triangular matrices was computed via double fusion and fed into the Bayesian spatio-temporal model as an informative prior for FC (not naïve FC but FC based on our model). We employed Markov Chain Monte Carlo methods for estimation using Metropolis-Hastings sampler implemented in PyMC 2.3.4². With the posterior distribution of each FC value, we considered any ROI pair with Pr(FC>0.4) > 0.5 as important³, equivalent to statistical significance in the conventional approach (denoted as AVG-FC) that is based on the averaged time series across voxels in each ROI. We also assessed which model was more robust to data decimation⁴.

RESULTS

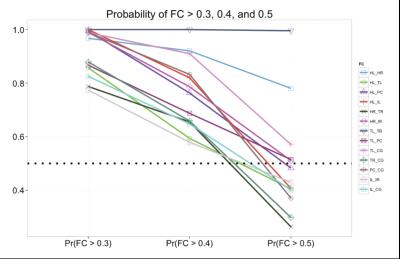
Table 2 summarizes the simulation studies, showing that our approach with a prior based on structural independence assumption (i.e., no structural connectivity) outperforms the conventional approach in which only rs-fMRI data are analyzed for FC estimation, in terms of mean squared errors (MSE). Regardless of the underlying spatial dependence, our approach achieves 54% reduction in MSE. Moreover, the simulation studies confirm that the conventional approach is more likely to increase false positive rates (i.e., more likely to reject the null hypothesis) with a smaller sample size, compared to our approach, i.e., with our approach false positive rate increases by 4% as sample size decreases from N=10 to N=5 while it increases by 55% with AVG-FC. As shown in Figure 1, our Bayesian approach identified 13 important FC estimates, while the conventional approach claimed that all of 28 FC values were statistically significant at FDR = 0.05. As shown in Figure 2, our approach is much more robust to data decimation than AVG-FC.

DISCUSSION/CONCLUSION

The study supports incorporating SC information into FC estimation while properly taking into account the underlying spatio-temporal correlation in fMRI data improve the accuracy and precision in FC estimation. More accurate and precise estimation of FC will enable scientists to correctly assess the relationship between FC and clinical information (e.g., brain disease status or progression).

Acknowledgements

NINDS R01NS075270