5372

Community detection in resting state functional connectivity networks beyond the resolution limit
Carlo Nicolini1, Cecile Bordier1, and Angelo Bifone1

1Center for Neuroscience and Cognitive Systems, Istituto Italiano di Tecnologia, Rovereto (TN), Italy

Synopsis

Graph-theoretical analysis has been widely applied to study the modular organization of brain functional connectivity networks. However, existing methods suffer from a fundamental resolution limit. Here, we propose and validate a novel, resolution-limit-free approach dubbed Asymptotical Surprise. Application of this method to human resting state networks reveals the presence of heterogeneously distributed modules, corresponding to neuroanatomically and functionally plausible networks. The finer partition afforded by Asymptotical Surprise enables a more accurate identification of connector hubs, the brain regions that are thought to be responsible for the integration of functionally segregated modules into a cohesive structure.

Introduction

Graph theory provides a powerful framework to investigate brain functional connectivity networks and their modular organization. However, most graph-based methods suffer from a fundamental resolution limit that may have affected previous studies and prevented detection of modules, or “communities”, that are smaller than a specific scale. Here, we propose Asymptotical Surprise, a novel, resolution-limit-free method for the study of weighted brain connectivity networks. We assessed the performance of this novel approach on synthetic networks endowed with planted modular structures, and compared it to some of the leading graph partitioning methods. We applied Asymptotical Surprise to weighted functional connectivity networks from resting state fMRI data, revealing a heterogeneous, multiscale community structure. In the light of the finer partition afforded by Asymptotical Surprise, we revised the classification of connector hubs, the brain nodes responsible for the integration of functional modules into a cohesive structure.

Methods

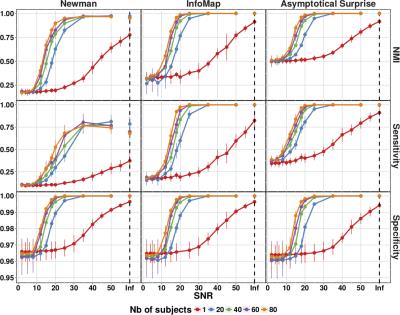
We used the extension of Surprise [1] to weighted networks recently proposed by Traag et al. [2]. A novel algorithm, dubbed PACO, was specifically developed to identify the optimal partition by maximization of Asymptotical Surprise. This approach was applied to ring-of-clique networks, and to synthetic LFR modular networks with different levels of correlation noise. The performance of Surprise was compared to that of Infomap [3] and Newman’s Modularity [4], two of the most widely applied methods, by calculating Normalized Mutual Information (NMI), Specificity and Sensitivity to the planted modular structures. Finally, we applied Asymptotical Surprise to benchmark human resting state functional connectivity networks from the brains of 27 healthy subjects [5]. Connector hubs were identified on the basis of within-module degree and partition coefficient [6] calculated for the same functional connectivity network with all three methods.

Results

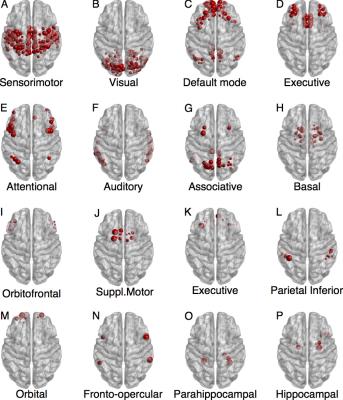
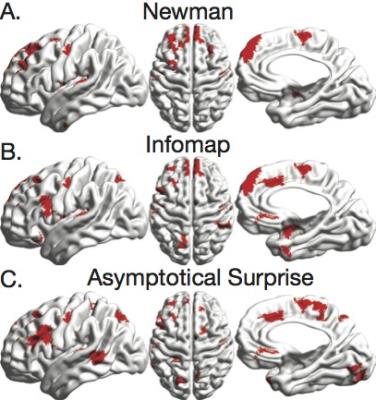
Fig. 1 shows NMI, Sensitivity and Specificity of Newman’s Modularity, InfoMap and Asymptotical Surprise in the detection of the modular structure of synthetic networks for different levels of noise and number of instances. Surprise presents the best Sensitivity to smaller modules while maintaining comparable Specificity to the other methods. Application of the three community detection methods to human resting state connectivity networks shows substantially different partitions (Fig. 2), with a wide distribution of modules ranging from large communities to singletons for Surprise and Infomap. The modules retrieved by Surprise correspond to functionally and anatomically plausible structures (Fig.3) including spatially extended cortical networks and smaller subcortical nuclei. The differences in the community structures detected by the three methods result in a different classification of the network’s connector hubs (Fig. 4), the nodes that are thought to be responsible for the integration of segregated functional modules into a cohesive structure.

Discussion

The presence of heterogeneously distributed modules in human functional connectivity networks may have important consequences for our understanding of the brain functional organization, and for the identification of integrative hubs. The connector hubs identified by our three methods present substantial differences, consistent with the idea that hub classification depends on community structure. By way of example, the Precuneus and the Cingulate Cortex are highlighted by Asymptotical Surprise, but not by resolution limited methods, as connector hubs. These are two key elements of the Default Mode Network that have been consistently identified as vulnerable regions in neurological diseases.

Conclusion

Asymptotical Surprise optimization proved superior to existing methods in terms of Sensitivity and accuracy in detection of planted structures in synthetic networks. Asymptotical Surprise revealed a complex modular structure of resting state connectivity, with communities of widely different sizes reflecting distributed functional networks alongside with smaller, anatomically or functionally defined modules. This evidence corroborates the idea that the resolution limit may have negatively affected current models of the brain modular organization and the identification of the hubs responsible for integration of functional modules.

Acknowledgements

This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 668863.

References

[1] Nicolini, C. & Bifone, A. Modular structure of brain functional networks: breaking the resolution limit by surprise. Sci.Rep. 6, 19250 (2016). ?

[2] Traag, V. A., Aldecoa, R. & Delvenne, J.-C. Detecting communities using asymptotical surprise. Phys. Rev. E 92, 022816 (2015). ?

[3] Rosvall, M. & Bergstrom, C. T. Maps of random walks on complex net- works reveal community structure. Proc. Natl. Acad. Sci. U.S.A. 105, 1118– 1123 (2008). ?

[4] Girvan, M. & Newman, M. E. J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. U. S. A. 99, 7821–6 (2002).

[5] Crossley, N. A. et al. Cognitive relevance of the community structure of the human brain functional coactivation network. Proc. Natl. Acad. Sci. U.S.A. 110, 11583–11588 (2013). ?

[6] Guimera, R., Nunes Amaral, L. A. & R. Guimera, L. A. Functional car- tography of complex metabolic networks. Nature 433, 895–900 (2005).

Figures

Figure 1: NMI, Sensitivity and Specificity of the three community detection al- gorithms applied to a power-law ring of clique network. SNR indicates Signal to Noise Ratio, and Inf the situation with a network structure unperturbed by noise. Number of Subjects indicates the different number of instances used to generate the group level network.

Figure 2: Adjacency matrix of the resting state functional connectivity net- work. The node indices have been reordered by module membership in each graph, and the red lines highlight the community structures obtained by A) Newman’s Modularity (Q = 0.4967); B) Infomap (L = 8.5173); C) Asymptotical Surprise (Sa = 5925.28).

Figure 3: Sixteen largest modules found by Asymptotical Surprise maximiza- tion in the resting state network overlaid on an MRI brain template. The modules are ranked by decreasing size, and named after corresponding functional networks previously identified by multivariate analysis of resting state fMRI data, or by the comprised anatomical districts.

Figure 4: Nodes presenting simultaneously large values of the participation coefficient and within-module degree (larger than 0.6 and 1.5, respectively) for the three community detection methods. These nodes are thought to represent the connector hubs responsible for the integration of the network’s modules.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
5372