5324

Evaluating the impact of SNR, sampling interval and number of samples on functional sensitivity using the General Linear Model framework

Nadège Corbin¹, Guillaume Flandin¹, Oliver Josephs¹, Nick Todd², Karl J Friston¹, and Martina F Callaghan¹

¹Wellcome Trust Centre for Neuroimaging, UCL Institute of Neurology, London, United Kingdom, ²Department of Radiology, Brigham and Women’s Hospital, Harvard Medical School, Boston, MA, United States

Synopsis

In fMRI, functional sensitivity is dictated by many factors related to the data acquisition scheme, most notably image SNR, temporal resolution and the number of samples acquired. Advanced acquisition techniques, such as 2D multiband imaging, are popular for fMRI studies because they afford the possibility of greatly increasing temporal resolution allowing more samples to be acquired per unit time, but at the cost of image SNR and increased temporal auto-correlations. This study uses the General Linear Model framework to disentangle these effects and determine the net impact on functional sensitivity, as parameterised via temporal SNR and t-scores.

Introduction

In fMRI, the most common method of detecting task-induced BOLD activation in data Y is via voxel-wise (mass univariate) general linear models (GLM): $$Y=X\beta+\epsilon, \epsilon\sim\mathcal{N}(0,\sigma^2V)$$ X is the GLM’s design matrix. Each row represents a single observation (i.e. acquisition volume). Each column represents an explanatory variable, for which $$$\beta$$$ constitute the regression coefficients. We assume $$$\epsilon$$$ to be Gaussian-distributed error with zero-mean and covariance $$$\sigma^2V$$$. To evaluate the significance of an effect of interest, $$$c^T\beta$$$, (c is a contrast vector of weights), a t-score is calculated:$$t=\frac{c^T\widehat{\beta}}{var(c^T\widehat{\beta})}=\frac{c^T\widehat{\beta}}{\widehat{\sigma}\sqrt{c^T(WX)^-(WX)^{-T}c}}=\frac{c^T\widehat{\beta}}{\widehat{\sigma}\eta}$$ $$$\widehat{\beta}=(WX)^-WY$$$ are maximum likelihood estimates. “-” denotes pseudoinverse. $$$W$$$ the whitening matrix, is defined as $$$W^TW=V^{-1}$$$. $$$V$$$ is a linear combination of a fixed set of covariance components modelling a mixture of white noise and a first-order autoregressive process¹. Inference is performed by comparing the computed t-score with a statistical threshold at a nominal significance level.

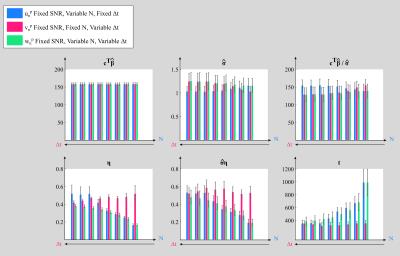
Multiband acquisitions afford increased temporal resolution^2-4 allowing more samples to be acquired for the same acquisition time and enabling physiological and BOLD signals to be better separated. Drawbacks include reduced SNR (lower steady-state magnetisation), increased g-factor (unfolding penalty) and greater temporal auto-correlation. Here we examine how number of samples (N), sampling interval (Δt) and multiband factor (MB) affect functional sensitivity by quantifying their effects on components of the t-score testing the mean (Fig.1).

Methods

Task-based fMRI data were acquired for ~8mins, on 10 subjects, with MB=1,2,4,8, using the CMRR sequence (R012, https://www.cmrr.umn.edu/multiband/) summarised in Fig.2. Using SPM12, time series were realigned, smoothed, co-registered with a T1-weighted image, normalized to MNI space. To distinguish increasing N from temporal resolution, under constant SNR, several series were derived from the original MB8 series (Fig.3). All GLM design matrices comprised mean, high-pass filter (cut-off=128s), motion and stimuli-specific regressors. Physiological corrections were not performed. The t-score testing the mean and its constituent components were estimated. Each mean metric within grey matter was averaged across subjects.

Results - Analysis of time series derived from MB=8 data to avoid confounds of varying SNR

Increasing N (blue,Fig.1): The mean estimate is independent of N whereas the variance estimate slightly increases, resulting in a tSNR decrease. Since $$$\widehat{\sigma}$$$ is taken to be an unbiased estimate, it is more accurately estimated with higher N. The tSNR is therefore interpreted as being artificially high for low N. η greatly decreases, increasing the t-score.

Decreasing Δt (red,Fig.1): As Δt decreases, but >1.5s, the variance estimate remains stable, while η increases because of increased auto-correlation in the data. For Δt<1.5s, the variance decreases, increasing tSNR. η is also under-estimated, because of temporal correlations remaining in the data. The t-score initially decreases (Δt>1.5s) as expected but is then over-estimated.

Increasing N and decreasing Δt (green,Fig.1) for a fixed acquisition time, leads to an increase in t-score since dominated by the effect of increasing N.

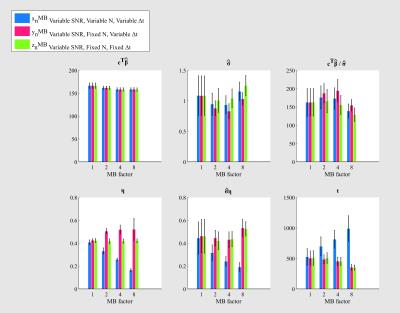
Results - Analysis of time series acquired with varying MB factor

Increasing MB, while fixing Δt and N (green,Fig.4) reduces the mean signal (reduced steady-state magnetisation) and increases the noise variance (g-factor penalties), without changing η. The overall result is a lower estimated tSNR and t-score.

Increasing MB, while decreasing the Δt (red,Fig.4): The noise variance is likely under-estimated for high MB (due to remaining temporal auto-correlations). The tSNR is biased by this under-estimation such that MB4 appears to have highest tSNR. The t-score decreases with increasing MB, though may still be over-estimated.

In typical imaging scenarios, increasing MB is accompanied by decreasing Δt and, assuming a constant overall acquisition time, increasing N (blue,Fig.4). The net effect is decreasing tSNR. However, the increase in N dominates (via η), such that t-scores greatly increase.

Discussion

Many studies assess functional sensitivity as tSNR per unit time (i.e. $$$tSNR*\sqrt{N}$$$, assuming fully independent data). However, this over-estimates the functional sensitivity improvement by failing to account for temporal auto-correlations and the effective degrees of freedom of the data (last rows, Fig.1). The GLM-derived t-score testing the mean estimates the mean signal relative to its estimated variance, accounting for temporal auto-correlations, giving a more reliable measure of functional sensitivity. However, for very short TR, the AR(1) plus white noise model (used here) is not guaranteed to sufficiently model temporal auto-correlations.

Conclusion

The key insight from this analysis is that improving functional sensitivity is not simply a matter of reducing the amplitude of random fluctuations (that may be irreducible if physiologically-mediated). More interesting is how efficiently both signal amplitude and random fluctuations can be estimated. In other words, one has to quantify the uncertainty about signal estimates (via standard error) and uncertainty about the standard error (via statistical degrees-of-freedom). This framework can be used to evaluate the impact of different acquisitions/data-processing schemes, e.g. our analysis shows that MB profoundly changes the degrees-of-freedom (inverse η).

Acknowledgements

The Wellcome Trust Centre for Neuroimaging is supported by core funding from the Wellcome Trust 091593/Z/10/Z.

References

[1] K. J. Friston, W. Penny, C. Phillips, S. Kiebel, G. Hinton, and J. Ashburner, “Classical and Bayesian inference in neuroimaging: theory,” NeuroImage, vol. 16, no. 2, pp. 465–483, Jun. 2002.

[2] K. Setsompop, B. A. Gagoski, J. R. Polimeni, T. Witzel, V. J. Wedeen, and L. L. Wald, “Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty,” Magn. Reson. Med., vol. 67, no. 5, pp. 1210–1224, May 2012.

[3] C. Preibisch, G. Castrillón, M. Bührer, and V. Riedl, “Evaluation of multiband EPI acquisitions for resting state fMRI,” PLoS ONE, vol. 10, no. 9, 2015.

[4] N. Todd, S. Moeller, E. J. Auerbach, E. Yacoub, G. Flandin, and N. Weiskopf, “Evaluation of 2D multiband EPI imaging for high-resolution, whole-brain, task-based fMRI studies at 3T: Sensitivity and slice leakage artifacts,” NeuroImage, vol. 124, pp. 32–42, 2016.

Figures

Fig.1: Description of the constituent components of the t-score, which were separately examined in order to investigate the estimate of the signal amplitude as well as our uncertainty in it, both of which will dictate functional sensitivity.

Fig.2: Protocol parameters of the Multiband acquisitions performed on 10 subjects. The last two rows quantify, relative to MB=1, the temporal SNR weighted by the square root of N and the t-score testing for the signal mean. The former is often used to evaluate the functional sensitivity of acquisition schemes, but as can be seen, this will result in an overestimation.

Fig.3: Description of the series used for subsequent analysis: Each native multiband acquisition, x_n^MB, n indexing the sample in the time series, is used to create two others: y_n^MB has a fixed number of samples (N), while z_n^MB has both fixed N and sampling interval (Δt) thereby allowing the impact of variable image SNR to be isolated. In order to remove the effect of variable image SNR, three additional sets of 8 time series were derived from the data acquired with MB=8: u_n^p and v_n^p are used to evaluate the impact of increasing N and decreasing Δt , respectively, in isolation, while w_n^p allows the combination of both effects to be evaluated.

Fig.4: Bar plots of each component of the t-score as described in Fig1. In order to remove the effect of variable image SNR, the time series analysed here are derived from the data acquired with MB=8. The effect of increasing N (left to right) for a fixed Δt is described in blue. The effect of decreasing Δt (left to right) for a fixed N is described in red. The combination of both is described in green. The error bars denote the standard deviation of the mean parameter within grey matter across subjects.

Fig.5: Bar plots of each component of the t-score as described in Fig 1. These time series have been derived from data acquired with four different MB factors as described in Fig.3. The effect of increasing the MB factor without altering N or Δt is described in green. The effect of increasing the MB factor without altering N but decreasing Δt is described in red. Finally, the typical combination of increasing the MB factor while decreasing Δt and increasing N is shown in blue. The error bars denote the standard deviation of the mean parameter within grey matter across subjects.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

5324