5271
The neurovascular fingerprint of BOLD bSSFP: the impact of vessel size, orientation and intravascular contributionKlaus Scheffler1,2, David Kleinfeld3,4, Philbert Tsai3, Mario Báez-Yánez1, and Philipp Ehses1
1MPI biol Cybernetics, Tübingen, Germany, 2Department of Biomedical Magnetic Resonance, University of Tübingen, Tübingen, Germany, 3Department of Physics, University of California at San Diego, San Diego, CA, 4Section of Neurobiology, University of California, La Jolla, CA
Synopsis
The neurovascular fingerprint of BOLD (blood oxygen level dependent) bSSFP (balanced steady-state free precession) is analyzed by Monte Carlo simulations for different vessel geometries and on a vectorized vessel data set of mouse parietal cortex. The results support that bSSFP yields vascular properties similar to those found with spin echo BOLD, a small intravascular signal contribution except for larger vessels, and a high selectivity to microvessels.
PURPOSE
Using
Monte Carlo simulations and measurements at 9.4T we analyze the vascular
fingerprint of BOLD bSSFP for different vessel geometries and for a vectorized vessel data set of the mice
parietal cortex measured with two-photon laser scanning microscopy at
1 µm isotropic resolution. In particular, we investigated the vessel diameter
selectivity for different repetition times, the intravascular signal
contribution for different blood volume (BV) fractions, the
orientation-dependency of vessels to the main magnetic field B0 for
different vessel diameters, and the BOLD-sensitivity of bSSFP across different
cortex layers and orientation to B0.
INTRODUCTION
A still somewhat open question is the origin
of signal formation in pass band BOLD bSSFP, which is of crucial importance to
interpret the quality of BOLD data with respect to the underlying neurovascular
point spread function. We use the Monte Carlo simulation methods of Bieri1,
Miller2 and Kim3 to analyze further aspects of the
neurovascular fingerprint of bSSFP.
METHODS
Relative signal changes (S0-S)/S0
of intra and extravascular contributions, where S0 is the steady
state signal without any susceptibility differences between vessel and tissue,
and S is the reduced signal generated by a susceptibility difference of Dc = 0.33x10-7 at 9.4T, were calculated
by Monte Carlo simulations for parallel and randomly oriented cylinders as well
as for a vectorized data set of the mice
parietal cortex4. Experimental data have been acquired at 9.4T on
healthy volunteers.
RESULTS
BSSFP shows a peak selectivity around small vessel radii that depends on
the chosen TR (Figure 1). With increasing TR the selectivity shifts to larger
vessels and the peak signal change is heavily increased, i.e., by a factor of
3-4 going from TR=5ms to 15 ms. Also, for longer TR (> about 10 ms) the
contribution from larger vessels (> 100 mm)
strongly increases to up to 50% of the peak signal.
Figure 2 gives an overview on the relation of intra and extravascular
signal contribution for three different vessel radii, and as a function of BV.
For a vessel radius of 5 mm
the intravascular contribution is negligible up to a BV of 20%, and up to a BV of
10% for 50 mm vessels. For a vessel >200
mm the overall signal change
is much smaller compared to 5 mm
vessels if BV is below 5%. This again reflects the small vessel selectivity of
bSSFP if BV is below 5%, which is the case within the cortex excluding surface
vessels. A strong signal change is visible with very high BV or for a pure
intravascular signal found with pixels located fully within a vessel (right
panel in Figure 2).
In Figure 3, only parallel cylinders with a certain angle to B0
have been simulated. This mimics a very simplified model of parallel diving
(penetrating) veins and arteries oriented perpendicular to the cortical surface
and thus vary in their angle to B0. For gradient echo (GE),
basically all vessels exhibit a strong dependence of the signal change on the
orientation to B0. For bSSFP and spin echo (SE), the signal change
of only small vessels (1 to 10 mm)
depend on the angle to B0, larger vessels just give a very small
signal change.
Figure 4 shows simulations on a real neurovascular network4.
The frequency distribution for layers 1 to 6 is shown left, narrowing towards
deeper layers. The signal changes for GE, bSSFP and SE across layers is shown
right, with the underlying data set oriented parallel and perpendicular to B0.
For GE a very strong signal change increase can be observed towards the surface
layer 1 which is less pronounced for bSSFP and SE. A certain dependence on the
orientation to B0 is visible for all modalities, but is strongest
for GE. The effect on orientation is inverted going from the surface layer to
deeper layers, reflecting that surface vessels are mostly perpendicular to the
penetrating vessels.
CONCLUSION
The data of Figures 1 and 2 demonstrate that bSSFP is selective to small
vessels as long as BV is below 5%. The data of Figure 3 indicates the strong
dependence of larger vessels on their angle to B0, which is not visible for
bSSFP and SE. These simulations also support the angle dependent BOLD
sensitivity of GE as shown in Figure 5 in Gagnon´s paper5, as well
as the insensitivity of SE (and bSSFP) to orientational effects. The data of Figure
4 confirms the simulations based on parallel or randomly oriented cylinders, which
assume a simplified uniform deoxygenation of all vessels.
Acknowledgements
No acknowledgement found.References
1. Bieri O, Scheffler K. Effect of diffusion in inhomogeneous magnetic fields on balanced steady-state free precession. NMR Biomed. 2007; 20: 1–10. 2. Miller KL, Jezzard P. Modeling SSFP functional MRI contrast in the brain. Magn. Reson. Med. 2008; 60: 661–673. 3. Kim TS et al, Analysis of the BOLD Characteristics in Pass-Band bSSFP fMRI. Int J Imaging Syst Technol (2012) 22(1): 23–32. 4. Blinder P et. al. The cortical angiome: an interconnected vascular network with noncolumnar patterns of blood flow. Nature Neuroscience(2013), Vol 15, 7: 889-97. 5. Gagnon L et al. Quantifying the Microvascular Origin of BOLD-fMRI from First Principles with Two-Photon Microscopy and an Oxygen-Sensitive Nanoprobe. The Journal of Neuroscience (2015), 35(8):3663–3675. 6. Scheffler, K et al, High-resolution mapping of neuronal activation with balanced SSFP at 9.4 tesla, MRM (2015) 76, 163-171Figures

Figure 1.
Simulated vessel size selectivity of bSSFP for different repetition times TR,
blood volume of 2% and flip angle of 20°.
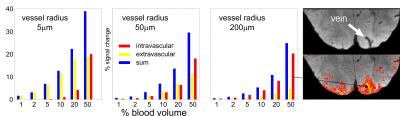
Figure 2.
Intravascular (red), extravascular (yellow) and total bSSFP signal change as a
function of increasing vascular blood volume and different vessel radius, using
a flip angle of 20° and TR=5ms. A significant intravascular signal contribution
only appears at a high bold volume fraction as shown right (bSSFP at 9.4T,
visual checker board stimulation, 0.6
mm isotropic resolution6) for a draining vein.
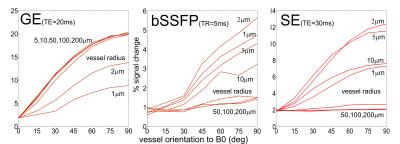
Figure 3.
GE, bSSFP and SE signal change as a function of vessel orientation relative to
B0, using a flip angle of 20° and TR=5ms for bSSFP, and TE=20ms for GE and
TE=30ms for SE.
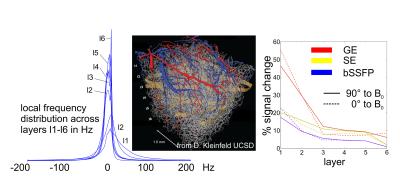
Figure 4. Monte Carlo simulation based on a real
neurovascular network for layers 1 to 6 (2-photon microscopy, 1 mm
isotropic resolution (7)). The local frequency distribution, left, assuming Dc = 0.33x10-7
at 9.4T, narrows with increasing layer depths. Middle:
visualization of the used vessel network4. The right panel shows
signal changes for GE, SE and bSSFP along layers being 0° (dashed) or 90° (solid)
oriented to B0.