5219

Spatial Resolution Analysis Comparing Density-Adapted and Conventional Projection Reconstruction in Chlorine-35 MRI at 9.4 T
Ruomin Hu1, Matthias Malzacher1, Mathias Davids1, Andreas Neubauer1, Simon Konstandin2, and Lothar R. Schad1

1Computer Assisted Clinical Medicine, Heidelberg University, Mannheim, Germany, 2MR-Imaging and Spectroscopy, Universty of Bremen, Bremen, Germany

Synopsis

35Cl MRI has been of interest for both human and animal in vivo applications to visualise chloride homeostatic changes. In this study we performed measurements of resolution phantoms at an isotropic resolution of 0.490 and 0.326 mm using scanner-equipped ultrashort echo time 3D (UTE3D) and newly implemented density-adapted 3D projection reconstruction (DA-3DPR) sequences with subsequent spatial resolution analysis. DA-3DPR images with visibly higher SNR are capable of resolving both gross and fine structures with more reliable signal distributions and more consistent rendition of structure shapes. Moreover, penalty-free radial oversampling leads to more extended artefact-free regions, allowing for smaller FOVs and reduced measurement times.

Purpose

35Cl MRI (spin = 3/2) has been of interest for both human1 and animal2 in vivo applications to visualise changes of the chloride homeostasis. The approach to face its challenges of low SNR and blurring is offered by conventional center-out non-Cartesian sampling techniques, currently available at many MR scanners. The density-adapted 3D projection reconstruction (DA-3DPR) technique has constant averaged sampling density in each spherical shell of k-space and seeks to offer further improvement over non-density-adapted techniques. DA-3DPR has been implemented for the first time on a 9.4 T preclinical system to the best of our knowledge.

In this study we performed measurements of resolution phantoms using DA-3DPR and scanner-equipped ultrashort echo time 3D (UTE3D) sequences. The aim was to demonstrate the superior spatial resolution capacity, SNR improvement and the potential of measurement time reduction of DA-3DPR.

Materials and Methods

Hardware: Experiments were performed on a 9.4 T preclinical MR system (BioSpec, Bruker, Germany) using a custom-made 16 rung low-pass birdcage 35Cl volume coil.

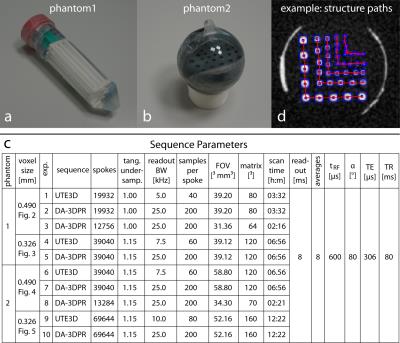
Resolution phantoms: Phantom1: 25 polystyrene rods in five groups of five (diameter&spacing = 2.50-0.75 mm) were attached inside a vial. Phantom2: 36 holes in five groups of nine (diameter&spacing = 3.5-1.0 mm) were drilled into a PVC cylinder fixed inside a sphere. Both phantoms (Figure1a,b) were filled with saline solution (3080 mM NaCl).

Sequence parameters: Parameter values are listed in Figure1c. Isotropic resolution (0.490 and 0.326 mm) was denoted as voxel size to avoid confusion with spatial resolution determined from modulation transfer functions (MTF)

Data evaluation: Images acquired with DA-3DPR were reconstructed using our algorithm; images of UTE3D were reconstructed using the scanner software. Each image is normalized to its maximum signal intensity (grey values (GV) between 0-1). For the resolution analysis5, 2D-Gaussian fit of the structure regions yielded the coordinates connecting the structure paths (Figure1d). GV values of phantom1 along the structure paths in the bar plots were reversed so that structures in both phantoms were represented by high GV. The differences between the mean high/low GV constituted the MTF data and were fitted by a logistic function. The threshold at which two structures were distinguished was set to 0.2.

Results and Discussion

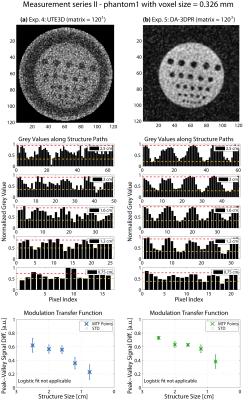
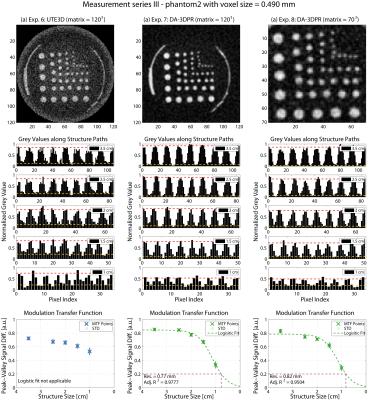
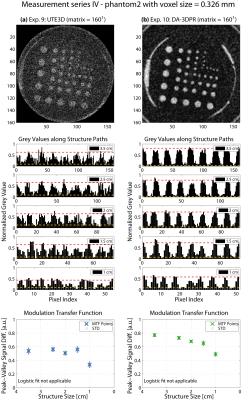
Results are grouped in Figure2-5. Overall, when comparing (a) with (b) of each figure, DA-3DPR images contain a significantly lower level of noise and suffer less from irregular blurring at the structure/background borders for the same total sampling time (tROI*spokes*averages). The bar plots show repetitive patterns of signal in- and decrease, indicating more accurately defined structure shapes, and substantially fewer uncorrelated signal spikes. Such spikes due to high noise level are falsely interpreted as high signal values and are responsible for artificially increasing the peak-valley signal differences for UTE3D especially for small structures. Comparing results of the same measurement series grouped in one figure, the peak-valley signal difference of the same structure is consistently higher for DA-3DPR when taking into account the uncertainty of the UTE3D values for small structures.

Reliable MTF fitting required a dispersed allocation of the MTF data (Figure2b-c,4b-c) and yielded a spatial resolution of 0.68/0.72 mm and 0.77/0.82 mm at voxel0.490mm for phantom1 and phantom2, respectively. If this criterion was unfulfilled, fitting resulted in low goodness of fit and was deemed inapplicable. It was the case for voxel0.326mm (Figure3,5), where even the smallest structures were reasonably well distinguished, and the remaining two UTE3D images (Figure2a,4a) due to overall mediocre peak-valley differences.

DA-3DPR enables radial oversampling without the trade-off of increased measurement time, leading to smaller Δk distances for a given trajectory, effectively enlarging the artefact-free FOV. Ringing artefacts can be discerned along the FOV edge of all UTE3D images. UTE3D supports artefact-free spherical FOVs with a maximal diameter of FOV1/3, with the volume outside the sphere being discarded during reconstruction, so that the artefact-free cubical FOVs of DA-3DPR can be at least 6/π-fold the size of UTE3D spheres at the same matrix size. For objects not complying to the circular image border of UTE3D, DA-3DPR requires smaller FOVs and reduced measurement times. For voxel0.490mm the DA-3DPR images with the minimalist FOV (Figure2c,4c) resulted in a comparable spatial resolution as those with the bigger FOV (Figure2b,4b).

Conclusion

Artefact-free DA-3DPR images with sub-millimeter voxel sizes were successfully acquired, and MTF fitting yielded spatial resolutions of 0.68-0.82 mm (voxel0.490mm). DA-3DPR images with visibly higher SNR are capable of resolving gross and fine structures with more reliable signal distributions and more consistent rendition of structure shapes for two opposite types of phantoms. Moreover, penalty-free radial oversampling leads to extended artefact-free regions, allowing for smaller FOVs and reduced measurement times

Acknowledgements

No acknowledgement found.

References

1. Nagel et al. In Vivo 35Cl MR Imaging in Humans: A Feasibility Study. Radiology. 2014;271(2):585-595

2. Baier et al. Chlorine and Sodium Chemical Shift Imaging during Acute Stroke in a Rat Model at 9.4 Tesla. Magnetic Resonance Materials in Physics, Biology and Medicine. 2014;27(1):71-79

3. Nagel et al. Sodium MRI Using a Density-Adapted 3D Radial Acquisition Technique. Magnetic Resonance in Medicine. 2009;62(6):1565-1573

4. Garvert. Design, Konstruktion und Charakterisierung eines Phantoms zur Auflösungsbestimmung eines Kleintier-MRT-Systems bei 1 Tesla. 2015. Bachelor’s Thesis. Heidelberg University.

5. Davids et al. Fully-Automated Quality Assurance in Multi-Center Studies Using MRI Phantom Meausurements. Magnetic Resonance Imaging. 2014;32(6):771-780

Figures

Figure 1: (a) Phantom1. Polysterene rods (diameter = 2.50-0.75 mm) were surrounded by saline. (b) Phantom2. Holes (diameter = 3.5-1.0 mm) in a PVC cylender were filled with saline. (c) Sequence parameters of UTE3D and DA-3DPR. (d) An example of structure paths. 2D-Gaussian fit region of each structure is indicated by the blue squares.

Figure 2: Measurement series I (Exp.1-3) with voxel0.490mm and phantom1. GV in the bar plots were reversed for phantom1. In (a,b) the same FOV with the same number of spokes were sampled. In (a) fine ringing artefacts are visible in the center; gross ringing is found at the edge of the automatically reconstructed, circular image. The restriction posed by the spherical FOVs of UTE3D overlapped with the gross ringing at the edge is non-existent for DA-3DPR; a minimalist FOV chosen in (c) results in comparable image quality and values of spatial resolution as in (b).

Figure 3: Measurement series II (Exp.4-5) with voxel0.326mm and phantom1. GV in the bar plots were reversed for phantom1. In (a,b) the same FOV with the same number of spokes were sampled. The high noise level of (a) is also reflected in the higher standard deviation of the MTF points. The GV along the structure paths shown in the bar plots in (a) also fail to clearly reveal the distribution of the structures, while those in (b) contain repetitive patterns of signal in- and decrease for all except the smallest structure size.

Figure 4: Measurement series III (Exp.6-8) with voxel0.490mm and phantom2. In (a,b) the same FOV with the same number of spokes were sampled. Uncorrelated signal spikes due to the high noise level in (a) are responsible for artificially increasing the peak-valley signal differences especially for smaller structures of a few pixels of width. Imaging objects not compliying with the circular image edge of UTE3D (such as the quadratic cross section of phantom2) benefit from the cubical FOV of DA-3DPR in terms of reduced FOV and measurement time. Fitting of MTF results in comparable spatial resolutions in (b) and (c).

Figure 5: Measurement series IV (Exp. 9-10) with voxel0.326mm and phantom2. In (a,b) the same FOV with the same number of spokes were sampled. GV in the bar plots in (a) are perturbed by oscillatory noise, whereas the distinction between peaks and valleys are evidently clearer in (b). Despite the fact that fitting of the MTF was inapplicable due to low dispersion of the values, the higher peak-valley GV differences in (b) nevertheless indicate a higher spatial resolution capacity.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
5219