5210

Slice-wise first-order shimming of the human spinal cord at 7T
S. Johanna Vannesjo1, Yuhang Shi1, Irene Tracey1, Karla L. Miller1, and Stuart Clare1

1FMRIB centre, Nuffield Department of Clinical Neurosciences, University of Oxford, Oxford, United Kingdom

Synopsis

Spinal cord imaging would benefit from the SNR increase at ultra-high field, to depict small structures inside the cord. However, higher background field strengths also increase susceptibility-induced B0 field distortions, causing image distortions and signal dropouts. To improve field homogeneity, we here implement slice-wise first-order shimming in the cervical spinal cord at 7T. The slice-wise shim settings were calculated based on a B0 field map and a semi-automatically generated spinal cord mask. We demonstrate that the slice-wise shims can improve signal levels in a high-resolution anatomical multi-echo GRE sequence.

Introduction

Spinal cord imaging would benefit from the SNR increase at ultra-high field, to image minute structures inside the cord. However, going to higher background fields also increases susceptibility-induced B0 field distortions. The spinal cord is particularly affected by the field profile around the neck, thorax and lungs, as well as by highly localized field distortions around each intervertebral junction. Resulting image distortions and signal dropouts constitute a significant barrier to ultra-high field spinal cord imaging.

Standard shimming approaches of applying up to 2nd- or 3rd- order spherical harmonic fields to the entire volume can only partially compensate for the static field inside the cord. In brain imaging, setting shims on a slice-wise basis has been proposed in order to improve field homogeneity locally1, and in the spinal cord a per-slice Z-gradient moment has been shown to reduce signal dropout in echo-planar imaging acquisitions at 3T2. Here, we explore the use of first-order slice-wise shimming for spinal cord imaging at 7T, and investigate the influence on a high-resolution anatomical gradient-echo (GRE) sequence.

Methods

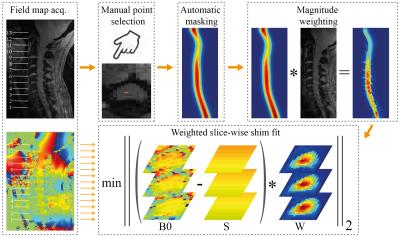
Imaging was performed in healthy volunteers on a whole-body 7T system (Magnetom, Siemens Healthcare) using a volume-transmit-, 16-channel receive cervical spine coil (Quality Electrodynamics). Slightly different protocols were implemented, and here we report results from one volunteer using a semi-automated pipeline to calculate slice-wise shims.

Prior to imaging, standard 2nd-order shimming was performed on the whole volume of interest. To calculate slice-wise shims, a sagittal B0 field map (13 slices, FOV 192x156mm2, in-plane resolution 1x1mm2, slice thickness 2mm, TE1/TE2 4.08/5.1ms, TR 620ms) was acquired. A spinal cord mask was extracted from the mean magnitude image, using the ‘sct_get_centerline’ function of the Spinal Cord Toolbox v1.1 3. The algorithm used a manually selected single voxel inside the cord as starting point. For each axial slice, first-order shim settings (B0,Y,Z) were calculated by a least-squares fit, weighted by the mask multiplied by the magnitude image (largely proton-density contrast). The fit included two slices on either side to yield sufficient conditioning for Z-shim calculation. Static field gradients in the left-right (X) direction were not expected, hence the corresponding shim term was not incorporated.

In order to evaluate the actually achieved field profile inside the spinal cord, axial B0 field maps were acquired without/with slice-wise shimming. Additionally, a multi-echo GRE sequence (13 axial slices, in-plane resolution 0.35x0.35mm2, slice thickness 3mm, TE [7.8, 15, 22, 29.4]ms, TR 532ms) used for anatomical imaging in the spine4 was acquired without/with slice-wise shimming. The change in average signal level in the root-sum-of-squares (RSS) across all echoes of the anatomical GRE was evaluated.

Results

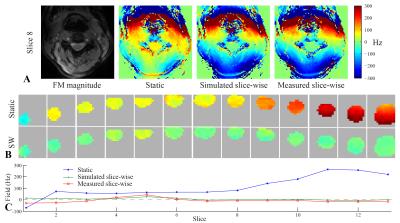
Measured field maps with slice-wise shimming closely matched simulated results (Fig. 2A). The field variation was reduced from around 330Hz with static shimming to 70Hz with slice-wise shimming (Fig. 2B,C). In the multi-echo GRE sequence, slice-wise shimming counteracted fast T2*-decay, yielding increased signal levels especially in later echoes (Fig. 3). The signal change depended on slice position, with particular improvement observed in slices towards the end of the FOV (Fig. 4). While most slices showed increased or unchanged signal levels, one slice had a marked negative net signal change. This arose as signal improvements in one area led to faster dephasing elsewhere. A similar pattern occurred in other slices showing net zero signal change (Fig. 3, slice 5). On average, the signal inside the spinal cord in the RSS images increased by 11% as compared to the mean signal level in the reference acquisition.

Discussion and Conclusions

As demonstrated here, slice-wise shimming has the potential to improve on the exceedingly difficult shim situation in the spinal cord at ultra-high field. However, it was observed that first-order shimming alone was not sufficient for field compensation in all slices. In a future step, we aim to investigate the use of higher-order spherical harmonic shim coils. Alternatively, shim coils specifically designed for spinal cord imaging may be utilized5.

To be integrated into standard imaging protocols, slice-wise shimming should ideally require as little manual intervention as possible. In this work, shims were calculated from a reference field map, using a semi-automatically generated mask. In future implementations a fully automatic spinal cord segmentation may be investigated6.

Improved shimming is especially important for sequences relying on long echo times, such as T2*-weighted anatomical and functional imaging. It may also prove instrumental for imaging large regions in the foot-head direction, such as the complete spinal cord or combined spinal cord/brain imaging7.

Acknowledgements

This project has received funding from the Wellcome Trust Strategic Award and from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 659263.

References

1. Blamire A, Rothman D, Nixon T. Dynamic shim updating: A new approach towards optimized whole brain shimming. Magn Reson Med 1996;36:159–165.

2. Finsterbusch J, Eippert F, Büchel C. Single, slice-specific z-shim gradient pulses improve T2*-weighted imaging of the spinal cord. NeuroImage 2012;59:2307–2315.

3. Cohen-Adad J, De Leener B, Benhamou M, et al. Spinal Cord Toolbox: an open-source framework for processing spinal cord MRI data. In Proceedings of the 20th Annual Meeting of OHBM, Hamburg, Germany, 2014. Abstract 3633.

4. Sigmund EE, Suero GA, Hu C, McGorty K, Sodickson DK, Wiggins GC, Helpern JA. High-resolution human cervical spinal cord imaging at 7 T. NMR Biomed. 2012;25:891–899.

5. Topfer R, Starewicz P, Lo K-M, Metzemaekers K, Jette D, Hetherington HP, Stikov N, Cohen-Adad J. A 24-channel shim array for the human spinal cord: Design, evaluation, and application. Magn Reson Med 2016;76:1604–1611.

6. De Leener B, Kadoury S, Cohen-Adad J. Robust, accurate and fast automatic segmentation of the spinal cord. NeuroImage 2014;98:528–536.

7. Finsterbusch J, Sprenger C, Büchel C. Combined T2*-weighted measurements of the human brain and cervical spinal cord with a dynamic shim update. NeuroImage 2013;79:153–161.

Figures

Fig. 1: Schematic overview of the procedure for calculating slice-wise shim settings. A sagittal field map is initially acquired. A mask covering the spinal cord is automatically calculated from the magnitude image, with the only manual input consisting of defining a single point inside the spinal cord. The mask is multiplied by the magnitude image to yield a weighting map (W) for the shim calculation. For each slice, optimal first-order (B0,Y,Z) shim settings (-S) are calculated by a weighted least-squares fit to the measured field (B0).

Fig. 2: A) Axial field maps acquired without (Static) and with slice-wise shimming (Measured slice-wise), shown together with a simulated slice-wise field map, constituting the static field map plus the calculated shim field. B) Measured field inside a manually defined spinal cord mask without (Static) and with (SW) slice-wise shimming. The color scale is the same as in A. C) Mean of the measured field inside the mask without (Static) and with slice-wise shimming (Measured slice-wise), shown together with the static field map plus the calculated shim field (Simulated slice-wise).

Fig. 3: Root-sum-of-squares (RSS) images and individual echoes of selected slices of a multi-echo GRE acquisition without (Static) and with slice-wise shimming (SW). In two of the displayed slices, slice-wise shimming considerably increased signal levels at later echo times within the whole area of interest. In the third slice, an improvement in the center of the spinal cord was accompanied by faster signal decay anteriorly, leading to approximately zero net signal change.

Fig. 4: A) RSS images of a multi-echo GRE acquisition without (Static) and with slice-wise shimming (SW). The bottom row shows difference images (SW - Static), scaled to +/- 10% of the maximum signal in the static case. B) The average signal difference in each slice within a manually defined spinal cord mask. The values are scaled to percent of the average signal inside the mask in the acquisition with static shimming

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
5210