5208

Shuffled Magnetization Prepared Multi-contrast Rapid Gradient Echo Imaging at 7T
Peng Cao1, Shuyu Tang1, Xucheng Zhu1, Andrew Leynes1, Angela Jakary1, and Peder Larson1

11Department of Radiology and Biomedical Imaging, UCSF, San Francisco, CA, United States

Synopsis

In this study, we aimed to explore accelerated acquisition of multi-contrast 3D images with different magnetization preparation times. We combined shuffled acquisition in k-space, parallel imaging, compressed sensing and pixel-wise low rank Hankel matrix reconstruction, achieving reconstruction of tens of multi-contrast 3D images from three 3-minute scans.

Purpose

In many gradient echo (GRE) imaging applications, the longitudinal magnetization is 'prepared' during the preparation pulse module to generate enhanced MRI contrasts. For example, the well-known magnetization prepared rapid gradient echo (i.e. MPRAGE) sequence is one of the most commonly used sequences for T1-weighted anatomic imaging. Recent studies also demonstrated applications of T2-weighting preparation for functional MRI, 1,2 MR angiography, 3 cardiac imaging 4 and quantitative T2 mapping. 5,6 Besides, the T1rho, magnetization transfer (MT), arterial spin labeling and many other MRI modalities involve the use of magnetization preparation pulses. However, magnetization preparation pulses perturb the steady state in conventional MRI sequences, imposing a challenge in the efficiency of segmented data acquisition. As shown by several recent studies, it is possible to reconstruct tens to hundreds of images with varied contrasts along the relaxation dimension of MRI signal with reduced scan time. 7–11 In the present study, we aimed to explore accelerated acquisition of multi-contrast 3D images with different magnetization preparation times. This was built upon a combination of several methods including shuffled acquisition in k-space, parallel imaging (via ESPIRiT 12), compressed sensing and pixel-wise low rank Hankel matrix reconstruction.

Methods

Adiabatic inversion, T2 and magnetization transfer preparation pulses: A standard hyperbolic secant pulse was used as the inversion pulse 13. A 0°-flip-B1-independent-rotation RF pulse, intersected by two ΔTE time intervals, 4,6,14,15 was used for T2 preparation. Two paired hyperbolic secant pulses were concatenated to produce 360°-flip spin locking for magnetization transfer preparation.

Magnetization prepared rapid gradient echo sequence: As shown in Figure 1a, magnetization preparation pulses were interleaved with the GRE segments. Multiple kx and ky lines were acquired per each magnetization preparation pulse (the Look-Locker method 16), generating a pseudo-random-ordered phase encoding table in real time.

Pixel-wise low rank Hankel matrix reconstruction enforces exponential curve in each pixel. For Hankel matrix reconstruction in combination with compressed sensing and parallel imaging, 12 the reconstruction problem in general can be written as

$$\bf \min_{I}\parallel{w_1(MFSBI-K)}\parallel_2^2 +\lambda_1\sum_{r∈Ω}\parallel{w_2 H[I(r)]}\parallel_* + \lambda_2{LLR(I)} + \lambda_3{TV(I)}$$ Eq. 1

I and K are related by linear operators: sampling mask M, Fourier transform operator F, coil sensitivity S and coil biased field B 17. The cost function enforces the consistency/fidelity of the estimated image I with the acquired k-space K and the weighting w1 for the fidelity. λ1, λ2 and λ3 are regularization parameters, in association with the pixel-wise nuclear norm for the Hankel matrix, H[I(r)] (r∈Ω the set of all pixels), total variation TV(I), and local low rank LLR(I) 8,18 with double threshold (described as the weighting w2 with its implementation shown in Fig. 1b bottom right). All the abovementioned regularizations were solved by the alternating direction method of multipliers algorithm, 19,20 using Berkeley MRI reconstruction toolbox (BART) software. 12

MRI protocol: Three volunteers were imaged on a 7T whole-body MRI scanner (GE Healthcare, Waukesha, WI). A 32-channel head coil (NOVA Medical) was used. Inversion-recovery prepared images were acquired with TE/TR=2.0/5.9ms, bandwidth=32.25Hz, FOV=220×220×192mm3 and FA=8°. T2-prepared images were acquired with TE/TR=2.0/5.9ms, bandwidth=62.5Hz, FOV=220×220×192mm3 and FA=5°. MT-prepared images were acquired with TE/TR=1.4/4.7ms, bandwidth=64.5Hz, FOV=256×256×256mm3 and FA=5°. All images had a matrix size of 128×128×128, NEX=1and scan time of 3 mintues .

Results

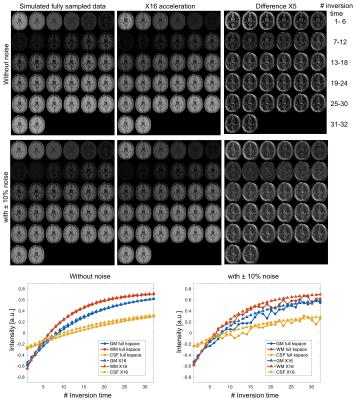
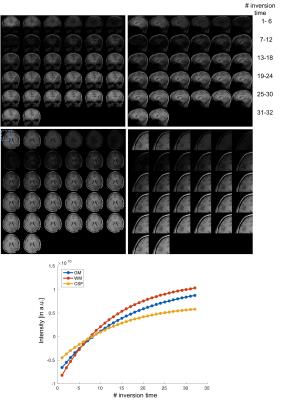
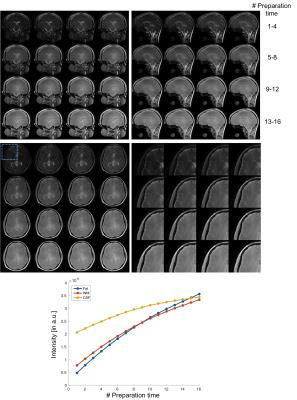
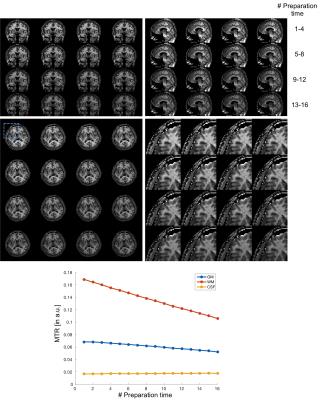
In simulation results (Figure 2), the contrast of accelerated images were comparable to those of fully-sampled ones. The proposed low rank Hankel matrix reconstruction also showed apparent de-noising effects on the T1 curves that contained the added white noise. In inversion-prepared in vivo results (Figure 3), the images with inversion times from 376 ms to 794 ms were mostly white matter enhanced with apparent T1 weighting. In T2-prepared in vivo results (Figure 4), the T2 contrast (e.g. the bright CSF signal) vanished with increasing preparation time, suggesting the need of resolving the T1 recovery for enhancing the T2 contrast. In MT-prepared in vivo results (Figure 5), the MTR decayed with increasing preparation time. Stronger MT contrast was observed at shorter preparation times. The non-mono-exponential time courses were also noticed, which demonstrated the applicability of proposed method for measuring MRI relaxations that deviate from mono-exponential decay.

Discussion and Conclusion

Simulation experiment demonstrated the robustness of the proposed method where a relatively high noise level was tested. The in vivo results further confirmed the capability of this method for recovering pixel-wise T1 recovery curves in a single magnetization-prepared scan. More importantly, the proposed method was clearly shown to improve the contrast of images in vivo while reducing T1 blurring in images.

In conclustion, proposed method can improve acquisition efficiencies for T1, T2 and magnetization transfer weighted MRI at high field using magnetization-preparation schemes.

Acknowledgements

No acknowledgement found.

References

1. Hua, J., Qin, Q., Van Zijl, P. C. M., Pekar, J. J. & Jones, C. K. Whole-brain three-dimensional T2-weighted BOLD functional magnetic resonance imaging at 7 Tesla. Magn. Reson. Med. 72, 1530–1540 (2014).

2. Solana, A. B., Menini, A., Sacolick, L. I., Hehn, N. & Wiesinger, F. Quiet and distortion-free, whole brain BOLD fMRI using t 2 -prepared RUFIS. Magn. Reson. Med. 0, n/a-n/a (2015).

3. Cukur, T., Lustig, M., Saritas, E. U. & Nishimura, D. G. Signal compensation and compressed sensing for magnetization-prepared MR angiography. IEEE Trans. Med. Imaging 30, 1017–1027 (2011).

4. Jenista, E. R. et al. Motion and flow insensitive adiabatic T2-preparation module for cardiac MR imaging at 3 tesla. Magn. Reson. Med. 70, 1360–1368 (2013).

5. Wang, G., El-Sharkawy, A. M., Edelstein, W. A., Schär, M. & Bottomley, P. A. Measuring T2 and T1, and imaging T2 without spin echoes. J. Magn. Reson. 214, 273–280 (2012).

6. Nguyen, T. D. et al. Feasibility and reproducibility of whole brain myelin water mapping in 4 minutes using fast acquisition with spiral trajectory and adiabatic T2prep (FAST-T2) at 3T. Magn. Reson. Med. 0, (2015).

7. Kecskemeti, S. et al. MPnRAGE: A technique to simultaneously acquire hundreds of differently contrasted MPRAGE images with applications to quantitative T1 mapping. Magn. Reson. Med. 1053, 1040–1053 (2015).

8. Tamir, J. I. et al. T 2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn. Reson. Med. 2016.

9. Benkert, T., Bartsch, A. J., Blaimer, M., Jakob, P. M. & Breuer, F. A. Generating multiple contrasts using single-shot radial T1 sensitive and insensitive steady-state imaging. Magn. Reson. Med. 73, 2129–2141 (2015).

10. Lee, D., Jin, K. H., Kim, E. Y., Park, S. H. & Ye, J. C. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn. Reson. Med. 0, 1–17 (2015).

11. Peng, X. et al. Accelerated exponential parameterization of T2 relaxation with model-driven low rank and sparsity priors (MORASA). Magn. Reson. Med. 0, (2016).

12. Uecker, M. et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 71, 990–1001 (2014).

13. SILVER, M. S., JOSEPH, R. I. & HOULT, D. I. Highly Selective Pi/2 and Pi-Pulse Generation. J. Magn. Reson. (San Diego, Calif 1997) 59, 347–351 (1984).

14. Nezafat, R., Ouwerkerk, R., Derbyshire, A. J., Stuber, M. & McVeigh, E. R. Spectrally selective B1-insensitive T2 magnetization preparation sequence. Magn. Reson. Med. 61, 1326–1335 (2009).

15. Hadrien, D. & Priti, B. Proc. Intl. Soc. Mag. Reson. Med. 23 (2015) 2393. ISMRM Proc. 2393 (2015).

16. Look, D. C. & Locker, D. R. Time saving in measurement of NMR and EPR relaxation times. Rev. Sci. Instrum. 41, 250–251 (1970).

17. Ahmed, M. N., Yamany, S. M., Mohamed, N., Farag, A. A. & Moriarty, T. A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data. IEEE Trans. Med. Imaging 21, 193–199 (2002).

18. Ong, F. & Lustig, M. Beyond Low Rank + Sparse: Multiscale Low Rank Matrix Decomposition. IEEE J. Sel. Top. Signal Process. 10, 672–687 (2016).

19. Afonso, M. V., Bioucas-Dias, J. M. & Figueiredo, M. A. T. An augmented lagrangian approach to the constrained optimization formulation of imaging inverse problems. IEEE Trans. Image Process. 20, 681–695 (2011).

20. Boyd, S., Parikh, N., E Chu, B. P. & Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 3, 1–122 (2011).

Figures

Figure 1 (a) MPRAGE sequences with segmented acquisition. Shuffled phase encoding caused the data with different inversion times to be mixed in a random order in the full k-space. (b) The scheme shows pixel-wise Hankel matrix low rank approximation, which enforced the exponential recovery curve in each pixel. “||” denotes concatenation.

Figure 2 Simulated inversion-recovery preparation data without and with ±10% noise. The images with 16-fold acceleration were similar with the full k-space ground truth. The differences were mostly found to occur on the edges and in CSF (longest T1). The proposed reconstruction method is robust against the ±10% noise level tested.

Figure 3 3D inversion-recovery prepared brain images (resolution = 1.7×1.7×1.5 mm3/pixel) with 32 inversion times (from 24 ms to 1486 ms with step size of 47 ms). The total scan time was 3 minutes and the acceleration factor was 16, including parrallel imaging and compressed sensing accelerations. The bottom left panel shows the T1 recovery curves from three single pixels representing GM, WM and CSF, respectively.

Figure 4 3D T2-prepared images (TE = 70 ms, resolution = 1.7×1.7×1.5 mm3/pixel and 3-minute scan) with 16 preparation times (from 33 ms to 492 ms with step size of 66 ms). The acceleration factor was 8, including parrallel imaging and compressed sensing accelerations. T2 contrast vanished with increasing preparation time, suggesting the need of resolving the T1 recovery for enhancing the T2 contrast.

Figure 5 3D MT-prepared brain images (resolution = 2×2×2mm3/pixel and 3-minute scan) with 8 preparation times (from 38 ms to 602 ms with step size of 38 ms). The acceleration factor was 16, including parrallel imaging and compressed sensing accelerations. MTR decays with the increase of preparation time. Stronger MT contrast was observed at shorter preparation times.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
5208