Synopsis

We investigate the performance that can be achieved by applying volume and slice shimming on the commonly-used Nova 8-channel transmit/32-channel receive head coil, whilst controlling the total transmit power, as a proxy for global SAR. Under this constraint, our results suggest that shimming on individual axial slices can significantly improve the achievable B1 field uniformity (39.0% ± 3.9%) for the same transmit power as normal quadrature mode.

Introduction

Static RF shimming through parallel transmission is a crucial tool for the mitigation of B1 inhomogeneities at high-field^1,2. Multi-slice acquisitions allow shimming to be performed separately on each slice, and this approach has previously been shown to outperform standard volume shimming at the expense of increased global SAR on a specially-designed, 15-channel transceiver coil³.

In this work, we investigate the performance that can be achieved by applying volume and slice shimming on the commonly-used Nova 8-channel transmit/32-channel receive head coil (Nova Medical Inc., Wilmington, USA), whilst controlling the total transmit power, as a proxy for global SAR. Under this constraint, our results suggest that shimming on individual axial slices can significantly improve the achievable B1-field uniformity for the same transmit power as normal quadrature mode.

Methods

B1 mapping was performed on six volunteers using the actual flip-angle imaging method⁴ on a Philips (Eindhoven, Netherlands) 7T Achieva scanner equipped with 8 transmit channels . The mapping of the B1-fields due to all 8-elements of the Nova transmit coil with an isotropic voxel size of 7mm and whole brain coverage took less than 5 minutes (TR₁= 40ms; TR₂= 160ms; TE= 4.6ms; FA= 40^o).

The coil can be driven in quadrature mode by applying a set of equal transmit amplitudes with differing phase offsets on each of the eight channels, yielding a B1-field with characteristic central brightening. The quadrature-mode B1-field was also mapped on the same six volunteers.

To achieve improved uniformity via B1-shimming, the complex transmit channel weights ($$$w\in\mathbb{C}$$$) were optimised using a magnitude least squares approach with Tikhonov regularisation (see equation 1, where $$$S_i$$$ represents the coil sensitivities at location $$$i$$$), and solved using a variable exchange method⁵. The channel amplitudes were subsequently scaled to yield a mean B1 field equal to the target field $$$b$$$.

$$\min_{w}\bigg( \sum_{i\in ROI}|||S_i w|-b||^2 + \beta ||w||^2 \bigg)\quad\quad(1)$$

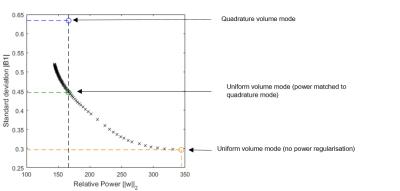
To match the transmit power between a B1-shim selected for B1 uniformity (uniform shim) and quadrature mode, the regularisation parameter $$$\beta$$$ in Eq. [1] was suitably adjusted. In effect, the L-curve of solutions (see Figure 1) was traversed until the nearest power-matched solution was found. For the extreme case of no power regularisation, $$$\beta$$$ was set to zero. The total optimisation time was less than one-minute in all cases.

Numerical simulations (FDTD) of electromagnetic fields produced by the coil elements in human head models (male and female) were provided by the coil manufacturer for an isotropic voxel size of 2mm. These were used to generate 10-gram average SAR maps in order to quantify local and global SAR for different sets of shim weights.

Results

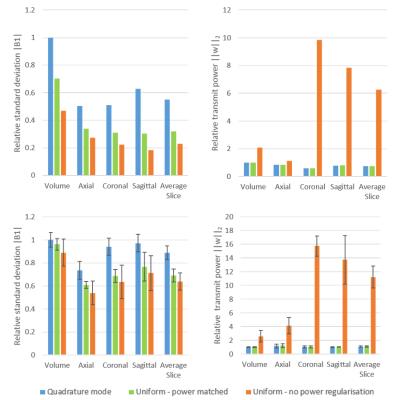
Calculations on the in vivo data showed that RF shimming over the whole volume provided no significant reduction in the standard deviation of the B1 field compared to quadrature mode (Figure 2). For the same total power as quadrature mode, axial slice-by-slice shimming provided the largest improvement in uniformity, with a change in standard deviation of 39.0% ± 3.9% from volume quadrature mode. Coronal and sagittal slice-by-slice shimming also gave improvements of 31.1% ± 4.6% and 23.3% ± 8.7% respectively.

It can be seen that removing power regularisation can slightly reduce the standard deviation further (standard deviation improvement over volume quadrature mode: axial: 46.0% ± 4.4%, coronal: 36.4% ± 6.1%, sagittal: 28.8% ± 6.8%), but this improvement comes at the expense of a dramatic increase in the transmit power, particularly for coronal and sagittal slice shimming (Figure 2).

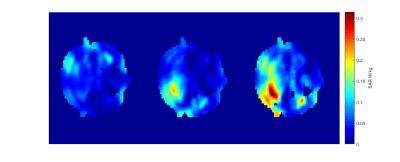
For the numerical simulations, with power regularisation, shimming over the axial slices again resulted in the greatest improvement (73.0% improvement in uniformity, as compared to quadrature volume mode). Global and local (Figure 4) SAR increased in this instance by 12.0% and 21.3% respectively. Without power regularisation, these values rise to 87.2% and 72.3%.

Discussion

These results show the sub-optimal performance of quadrature volume mode for head imaging. Slice-by-slice shimming (even in quadrature mode) provides substantial improvements in the B1-field uniformity, which can be further improved at the same transmit power by use of a shimming optimisation algorithm.

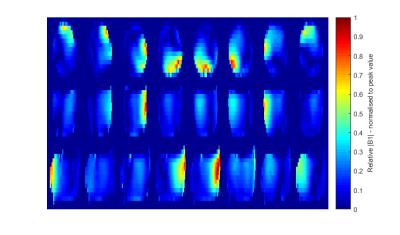
Shimming on axial slices is preferential for the Nova 8-channel coil due to its rotational symmetry, whereby each channel provides an equal contribution to the total B1 field in an axial plane. Coronal and sagittal slices experience poorer channel coverage when unit power is defined for each coil, with fewer than 8 coils dominating (Figure 3). In the unlimited power scenario– the optimisation seeks to increase the power through these other channels, resulting in the large total transmit power (and hence SAR) observed in Figure 2 for coronal and sagittal slices.

Acknowledgements

References

1. Katscher U. et al. (2006): NMR in Biomedicine. 19(3): 393-400

2. Van de Moortele PF. et al. (2005): MRM. 54(6): 1503-1518

3. Curtis A. et al. (2012): MRM. 68(4): 1109-1116

4. Yarnykh VL. (2007): MRM. 57(1): 192-200

5. Setsompop K. et al. (2008): MRM. 59: 908-915