5192
A new Phase Unwrapping Method Based on Wraps Identification and Local Surface Fitting for Water-Fat Separation1School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu, People's Republic of China, 2School of Biomedical Engineering and Guangdong Provincial Key Laboratory of Medical Image Processing, Southern Medical University, Guangzhou, People's Republic of China, 3Philips Healthcare, Guangzhou, People's Republic of China
Synopsis
The phase information is widely used, for example water-fat separation, susceptibility imaging, etc. The phase-unwrapping methods are generally needed to estimate the underlying true phase from the principal period (-π, π]. While current phase-unwrapping methods are affected by noise, rapid phase change and disconnected regions. This paper presents an algorithm combined a wrapping identification scheme by thresholding the difference map between the local variations between phasor and wrapped phase, with the local polynominal surface fitting to merge the disconnected components and estimate the phase value of residual pixels in quality guidance region-growing way. The results demonstrate the proposed method provides an accurate and reliable unwrapped results and has potential application to phase-related MRI in practice.
Target Audience:
Researchers who are interested in phase-unwrapping and water-fat separation.Purpose:
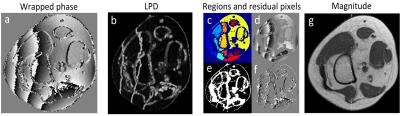
The clinical demands of MR phase information rapidly increase [1], such as water-fat separation. However, the acquired phase is usually wrapped into the principal period (-π, π] rad (e.g., arctan2), therefore phase-unwrapping methods are needed to estimate the underlying true phase. While current phase-unwrapping methods are affected by noise, rapid phase change and disconnected regions. In this paper, we present a new 2D phase unwrapping algorithm that combines a wrapping identification scheme by thresholding the local phase difference (LPD) map which is the root square of phase difference between the current pixel and those pixels in a neighboring window of size k × k (Fig. 1b), with the local polynominal surface fitting (LPSF) to merge the disconnected components (Fig 1c) and estimate the phase value of residual pixels (Fig 1e) in quality guidance region-growing way.Methods:
The proposed method first identifies the locations where wrapping happened by LPD thresholding. The threshold is calculated by considering the noise factor and the ratio of phase difference larger than π, and written as: $$LPD_A(num-fix(R_E*num))$$, where LPDA( ) is an operation to arrange the pixels of LPD in ascending order, fix( ) is a function to obtain the nearest minimum integer, num is pixels number of LPD. RE = RI + RN represents wrapping level, where RI is the ratio of phase difference between adjacent pixels is larger than π, RN depends on noise. After such, the input phase would be segmented into two parts: discontented regions in which phase is smooth, and residual pixels in which wrapping happen. Then, inter-region unwrapping is performed by using LPSF. The unwrapping begins with the largest region, and proceeds with the closest regions. At last, the unwrapped regions are used to estimate phase values of residual pixels in region-growing way with 9 stacks (first-in, first-out) by the quality guidance LPSF. LPD is employed to guide the unwrapping sequence of residual pixels, the pixel with minimum value at the edge of the merged regions is thought as the initial seed for residual pixel unwrapping. An iteration strategy to select RE is adopted here to improve the applicability of the proposed algorithm. An empirical value of 0.3 is chosen as initial RE with 0.1 subtracted after each iteration, and 3 iterations is enough to achieve a satisfying result in a reasonable time.
To evaluate the performance of the proposed method under different SNRs, ring-shaped data with 12 sectors whose magnitude increasing from 10 to 120 were synthesized on a 256×256 grid, the phase is a Gaussian surface with an SD of 50 pixels and height of 20 rad. Gaussian noise with an SD of 20 rad was added, and SNRs in different vectors are from 0.5 to 6 with an increment of 0.5.
Two knee and one ankle 3-point spin-echo Dixon [3] datasets were obtained from a 0.35-T permanent magnet MR scanner (Xingaoyi Company, Ningbo, China). Ten volunteers were scanned with parameters: TE/TR = 28/580 ms, matrix size 256×256, FOV = 240×240 mm2. The volunteers gave their informed consent following Research Ethics Committee approval. The performance of the proposed method was compared with PRELUDE [2].
Results:
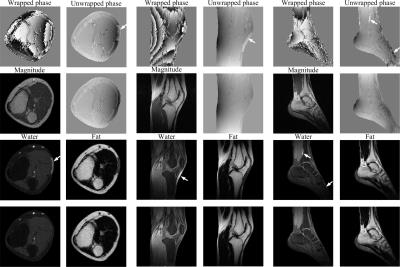
Figure 2 displays the performance evaluation under different SNRs. The proposed method obtained a satisfactory result map even at a low SNR of 0.5, while the result of PRELUDE have wraps in low SNR regions where SNR is lower than 1.5. Figure 3 shows some water-fat separation examples of PRELUDE and the proposed method, respectively. Apparent wrapping can be seen in the results of PRELUDE (white arrows in first row), which not only appears in the center of mask, but also in low SNR regions, leading to obvious water/fat swaps (white arrows in third row). However, the results of the proposed method did not produce swaps on the same data. For all real experiments, PRELUDE result 7, 24 and 18 swaps, while the proposed method produced 2, 0 and 3 swaps out of the corresponding 100 sagittal knee, 100 transverse knee and 50 sagittal ankle images, respectively.Discussion and conclusion:
The proposed method is a novel phase unwrapping method based on a wrapping identification scheme and LPSF technique. Both simulation and in vivo results demonstrates that the proposed method can correctly unwrapped phase even in the presence of low SNR and disconnected regions.
In conclusion, the proposed method can provide an accurate and reliable unwrapped results and have potential application to phase-related MRI in practice.
Acknowledgements
No acknowledgement found.References
[1] Ma J. JMRI: 28 (3): 543-558, 2008.
[2] Jenkinson M. MRM: 49: 193-197, 2003.
[3] Glover G, et al., MRM: 18 (2): 371-383, 1991.
Figures