5188
Water and fat separation using a Gauss-Newton Trust-Region based algorithm1Institute for Biological and Medical Engineering, Schools of Engineering, Medicine and Biological Sciences, Pontificia Universidad Catolica de Chile, Santiago, Chile, 2Biomedical Imaging Center, Pontificia Universidad Catolica de Chile, 3Electrical Engeneering Department, Pontificia Universidad Catolica de Chile, Santiago, Chile, 4Biomedical Imaging Center, Pontificia Universidad Catolica de Chile, Santiago, Chile, 5Radiology, University of Wisconsin, Madison, WI, United States, 6Medical Physics, University of Wisconsin, Madison, WI, United States, 7Radiology Department, School of Medicine, Pontificia Universidad Catolica de Chile, Santiago, Chile
Synopsis
We propose an algorithm based on a Gauss-Newton Trust-Region algorithm that estimates the field map and water and fat concentrations in two steps for all pixels at once. The results are comparable to those obtained with the state-of-art methods.
Introduction
Several methods have been proposed for water and fat separation1,2,3. Usually, most methods initially estimate the field map, and iterate between two steps: computing the fat and water concentrations and refining the field map estimation for each pixel. The main difference among the methods is the selection of the initial estimate. For instance, some use a low resolution images (RG ideal), or a multi-resolution approach (Hierarchical Ideal) or Graph Cuts4. The purpose of this work is to present a simple methodology that allows finding the field map in a single step for all pixels at once, which is then used to find water and fat species. The results are comparable to those obtained with the state-of-art methods.Methods
We consider the standard multi-peak model at each pixel$$ s_k e^{-2\pi i t_k \phi} = \rho_{\textrm{water}} + \rho_{\textrm{fat}}\sum_{\ell = 1}^{M} e^{2\pi i \Delta f_\ell t_k} $$where $$$s_k$$$ is the signal at echo-time $$$t_k$$$, $$$\rho_{\textrm{water}}$$$ and $$$\rho_{\textrm{fat}}$$$ denote the water and fat concentrations, $$$M$$$ is the number of species used to model fat and $$$\Delta f_\ell$$$ is their chemical shift. $$$\phi$$$ denotes the field inhomogeneity. Note we recover the single-peak model by setting $$$M=1$$$. We have explicitly written the inhomogeneity in the left-hand side, as this makes explicit the linearity of right-hand side in the concentrations. In absence of noise, a reconstruction is obtained whenever $$$\phi$$$ makes the linear system consistent. To achieve this, one typically aims to make $$$P z(\phi)$$$ small, where $$$P$$$ is the orthogonal projector onto the orthogonal complement of the range of the associated matrix, and $$$z_k(\phi) = s_k e^{-2\pi i t_k \phi}$$$; clearly $$$Pz(\phi) = 0$$$ implies the associated linear system for the concentrations is consistent. For the whole image, we propose to solve$$ \boldsymbol{\phi}^\star = \arg\min_{\boldsymbol{\phi}}\,\, f(\boldsymbol{\phi}) := \frac{1}{2}\sum_{x}\| P z(\phi_x)\|_2^2 + \lambda R(\boldsymbol{\phi})$$where $$$R$$$ is a convex regularizer. Here we select the squared $$$\ell_2$$$-norm of the gradient with $$$\lambda = 1E-2$$$. The rationale for this, it is that we desire a smooth field in order to avoid phase wrapping artifacts, and classical choices, e.g., TV, allow for field discontinuities. Although the objective is non-convex, it can be represented as $$$f(\boldsymbol{\phi}) = g(T(\boldsymbol{\phi}))$$$ where $$$g$$$ is convex and $$$T$$$ is a smooth non-linear map. Problems of this form can be solved with a Gauss-Newton Trust-Region approach: at each iterate $$$\boldsymbol{\phi}_k$$$ we minimize a model for $$$f$$$ near the iterate over a $$$\ell_2$$$-trust-region to find the next one. The model is constructed by linearizing $$$T$$$ around the current iterate. This way, each trust-region problem can be solved efficiently. To allow a consistent comparison of results, we always choose $$$\boldsymbol{\phi}_0 = 0$$$, i.e., the results we report correspond to the local minimizer closest to the origin.
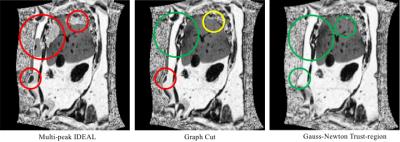
We tested our algorithm in 10 abdomen data set acquired in a clinical 3.0T MRI GE scanner. The data consist in 3D sagittal acquisition of abdomen, with the following MR acquisition parameters: 6 echoes, FOV=48.0x38.4x46.8cm, res=3.2x3.2x3mm, TR/TE=7.5ms/0.9ms, ∆TE=1.1ms. The more challenging slices were selected to test the algorithm, in particular those that shows severe water/fat swap in the IDEAL reconstruction. Fat fraction maps were obtained with our methodology and compared with Ideal, and Graph cut methods.
Results
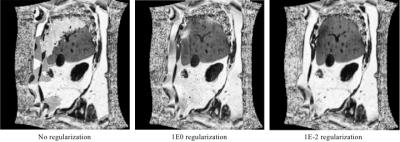
Figure 1 shows the result of a fat fraction map obtained with our method for different regularization weights. We observed that without any regularization there were swaps between water and fat in regions of high field inhomogeneities, while large weighting provided a solution with no swaps but at the expenses of smooth images. In general, a very small weight (1E-2) was able to avoiding swaps.Figure 2 compares the result of our method with multi-peak IDEAL and also with one of the state-of-the-art algorithm based on a Graph Cut formulation.
Discussion and Conclusion
We have proposed a simple approach that allows to separate water and fat images in a straightforward manner. This approach offers some advantages over existing methods. Firstly, the formulation is simple, requiring solving a single optimization problem to obtain the field map and subsequently the other variables of the model. Secondly, the algorithm works in all pixels at once, which allows us to regularize the solution and avoid swaps in areas of high field inhomogenieties. Thirdly, the $$$\ell_2$$$-norm squared of the gradient is enough to obtain results that are qualitatively similar to those obtained from multi-stage reconstruction methods. Although not shown here, the methodology can easily incorporate data from multiple coil, obtaining a single result for water and fat concentrations, and field map, eliminating the need to combine the results from different coilsAcknowledgements
This work was funded by the grant CONICYT FONDEF/I Concurso IDeA en dos etapas ID15|10284.References
1. Reeder SB, Wen Z, Yu H, Pineda AR, Gold GE, Markl M, Pelc NJ, Multicoil Dixon Chemical Species Separation With an Iterative Least-Squares Estimation Method. Magn Res Med. 2004;51:35-45.
2. Yu H, Reeder SB, Shimakawa A, Brittain JH, Pelc NJ. Field Map Estimation with a Region Growing Scheme for Iterative 3-Point Water-Fat Decomposition. Magn Res Med. 2005;54:1031-1039.
3. Yu H, McKenzie CA, Shimakawa A, Vu AT, Brau ACS, Beatty PJ, Pineda AR, Brittain JH, Reeder SB. Multiecho Reconstruction for Simultaneous Water- Fat Decomposition and T2* Estimation. J. Magn Res Imaging. 2007;26:1153-1161.
4. Hernando D, Kellman P, Haldar JP, Liang Z-P. Robust Water/Fat Separation in the Presence of Large Field Inhomogeneities Using a Graph Cut Algorithm. 2010;63:79-90.