5180
A novel method for Rapid 3D fat and water decomposition using a GlObally Optimal multi-surface Estimation (R-GOOSE)1Electrical and Computer Engineering, University of Iowa, Iowa City, IA, United States, 2Radiology, University of Iowa, Iowa City, IA, United States
Synopsis
A 3D Rapid, GlObally Optimal Surface Estimation (R-GOOSE) algorithm for fat-water decomposition in MRI is proposed. The fat-water separation is formulated as an optimization problem with data consistency and field-map smoothness penalty. The data consistency only contains exact minimizers from the fully discretized field-map value volume. The proposed method employs a connectivity-reduced graph construction that enables the new formulation to be solved efficiently. The method is validated by the 17 datasets from the 2012 ISMRM Challenge with thirty-fold computational gain compared to our previous method GOOSE while the high quantitative accuracy is maintained. Fat fraction maps obtained from the proposed method also provides a good marker for degenerative muscle diseases in newly collected lower limb datasets.
Purpose
The estimation of fat and water from multi-echo MR images is a classical problem. The non-linearity of the image model and the ambiguities often make the estimation from few numbers of echoes challenging. Iterative algorithms that exploit the smoothness of field map[1,2,3,4] are able to overcome the problem in simpler situations. However, none of the above algorithms are guaranteed to converge to the global optimum of the cost function, leading to fat-water or phase wraps in challenging applications. A single-step graph search algorithm termed as GOOSE[5], guaranteed to converge to the global minimum, was recently introduced. While this scheme was able to provide considerably improved results over the state-of-the-art, this scheme had a high computational complexity, restricting its application in large-scale 3D problems. Here, we introduce a new algorithm, which inherits the global optimality of GOOSE, while reducing the computational complexity by an order of magnitude.Methods
The fat-water signal at each pixel $$$\mathbf r = (x, y, z)$$$ can be mathematically expressed as a succession of images in different echo-times (ET): $$\underbrace{\begin{bmatrix}s(\mathbf r,t_1)\\\vdots\\s(\mathbf r,t_N)\end{bmatrix}}_{\mathbf s(\mathbf r)} = \underbrace{\begin{bmatrix} e^{-jf(\mathbf r) t_1} & \left(\sum_{i=1}^M \beta_i\,e^{j2{\pi}{\delta_i-f(\mathbf r)}\,t_n} \right)\\ \vdots & \vdots\\ e^{-jf(\mathbf r) t_N} & \left(\sum_{i=1}^M \beta_i\,e^{j2{\pi}{\delta_i-f(\mathbf r)}\,t_N} \right) \end{bmatrix}}_{\mathbf A_f(\mathbf r)}\underbrace{ \begin{bmatrix}\rho_{\rm water}(\mathbf r)\\\rho_{\rm fat}(\mathbf r)\end{bmatrix}}_{\boldsymbol \rho(\mathbf r)}$$
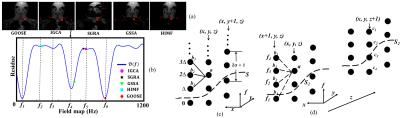
Classical methods aims to estimate the field $$$f(\mathbf r)$$$ by minimizing the criterion $$$D\left(f(\mathbf r) \right) = \min_{\boldsymbol \rho}\|\mathbf s(\mathbf r) - \mathbf A_{\mathbf f}(\mathbf r) \boldsymbol\rho\|^2$$$. GOOSE discretized the field-map at each pixel value onto a uniform grid $$$R_{f} = n\Delta$$$, where $$$\Delta$$$ is the grid spacing. It made the problem well-posed using an implicit smoothness constraint, illustrated in Figure 1(c). The global optimum of the constrained optimization problem was determined using a graph search algorithm. But the main drawback was the high computational complexity, resulting from the large number of graph layers.
In this work, we introduce a novel formulation that restricts the graph search to the local minima of $$$D\left(f(\mathbf r) \right)$$$ at each voxel. This results in far fewer graph layers, which considerably reduces the computational complexity. The algorithm still inherits the global optimality of GOOSE. The local minima of $$${\cal D}(f(\mathbf r))$$$, denoted by the set $$$\rm LM(\mathbf r)$$$, is determined using a fast discrete search. The field-map estimation is posed as the smoothness penalized 3D optimization problem: $$\{\hat{f(\mathbf r)}; \mathbf r \in G\} = {\arg \min_{\{\hat{f(\mathbf r)}; \mathbf r \in G\}}} \sum_{\mathbf r \in G}[{\cal D}(f(\mathbf r))+ \sum_{\mathbf s \in N(\mathbf p)}\mu_{\mathbf {rs}} {|f(\mathbf r)-f(\mathbf s)|^{2}}], ~~ f({\mathbf r}) \in {\rm LM(\mathbf r)}$$
Here, $$$N(\mathbf r)$$$ is the local neighborhood of the voxel $$$\mathbf r$$$ and $$$\mu_{\mathbf {rs}}$$$ are predefined weights. The first term is the data consistency cost, while the second encourages field-map smoothness.
To solve the above formulation, we build a graph whose nodes at each pixel are the entries of $$${\rm LM}(\mathbf r)$$$. The node costs are specified by $$${\cal D} (f(\mathbf r))$$$ and the smoothness costs are by $$$\mu_{\mathbf {rs}} {|f(\mathbf r)-f(\mathbf s)|^{2}}$$$, which are distributed between edges. The graph problem is solved using the graph construction introduced in [7]. Once the optimal field map is obtained, the fat and water concentrations are estimated as $$$\rho = (\mathbf A^{T}_f \mathbf A_f)^{-1} \mathbf A^{T}_f \mathbf{s}$$$.
Results
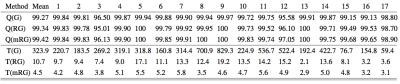
We first validate the proposed algorithm using the ISMRM metric across 17 datasets from the 2012 ISMRM Challenge7. We observe that the proposed scheme on average takes 10 seconds/dataset and provides an average score of 99.34%. We also implemented a multi-scale version of the algorithm similar to [8] to further reduce the computation time. Specifically, the field-map solution obtained from a down-sampled dataset is propagated to the finer scale. This further reduced the run time to an average of 4.5 seconds, while score improved marginally to 99.42%. See Table 1 for details. In Figure 2, a challenging case (Data 12) due to its SNR and the isolated 'island' of object (water) is shown. The proposed method successfully identified the island as water and achieves a score of 97.63%.
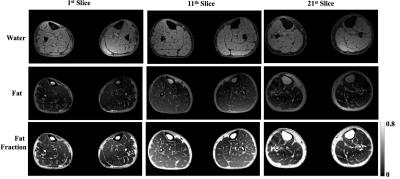
We are currently using the algorithm to evaluate fat fraction map as a biomarker for disease progression and treatment efficacy in neurodegenerative muscle diseases such as myotonic dystrophy (DM1) and Charcot-Marie-Tooth disease (CMT), which are characterized by fatty infiltration and muscular atrophy. An example from the study on a bilateral lower limb dataset, acquired with a gradient-echo-based 3-point Dixon sequence on a GE 750w scanner is shown in Figure 3.
Acknowledgements
No acknowledgement found.References
[1] Hernando D, Kellman P, Haldar JP, and Liang ZP. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magn Reson Med, 2010; 63:79–90.
[2] Berglund J, Johansson L, Ahlstrom H, and Kullberg J. Three-point Dixon method enables whole-body water and fat imaging of obese subjects. Magn Reson Med, 2010; 63:1659–1668.
[3] Lu W, Hargreaves BA. Multiresolution field map estimation using golden section search for water-fat separation. Magn Reson Med, 2008; 60:236–244.
[4] Tsao J and Jiang Y. Hierarchical IDEAL: Fast, robust, and multiresolution separation of multiple chem- ical species from multiple echo times. Magn Reson Med, 2012; 70:155–159.
[5] Cui C, Wu X, Newell JD, and Jacob M. Fat water decomposition using globally optimal surface estima- tion (goose) algorithm. Magn Reson Med, 2015; 73:1289–1299.
[6] Shay A, Bai J, Abramoff M, Wu X. Optimal Multiple Surface Segmentation with Convex Priors in Irregularly Sampled Space. https://arxiv.org/abs/1611.03059.
[7] http://challenge.ismrm.org/node/18
[8] Berglund J and Skorpil M. Multi-scale graph-cut algorithm for efficient water-fat separation. Magnetic Resonance in Medicine, 2016.
Figures