INTRODUCTION

Cerebral artery angiography is the mainly way to measure the degree of vascular stenosis for evaluating the seriousness of the intracranial atherosclerosis clinically. While research has confirmed that it would miss many fatal vascular lesions when only judge on the vascular stenosis degree¹. So it is necessary to develop direct imaging of the Intracranial artery vessel wall. MR vessel wall imaging is an emerging tool for evaluating intracranial artery disease and the only way to show the intracranial artery vessel wall noninvasively^{2, 3}. Since the special anatomical basis of cerebral arteries, intracranial artery vessel wall imaging faces several unique technical challenges. Our previous work on feature refinement has shown obvious effect in parallel MR imaging⁴. In this work, we implement the feature refinement strategy into the basic L1-SPIRiT framework⁵ to improve the sharpness and the contrast of MR vessel wall imaging.

METHOD

L1-SPIRiT is used to solve the reconstruction problem of the intracranial artery vessel wall, which is described as $$min⁡‖Dx-y‖^2+α_1 ‖(G-I)x‖^2+α_2 ‖Ψ(IFFT(x))‖_1$$ here, D is the operator that selects only acquired k-space locations, x is the entire reconstructed k-space data for all coils, y is the data acquired with arbitrary k-space sampling patterns, and the matrix G is a series of convolution operators that convolves the entire k-space with the appropriate calibration kernels, $$$Ψ(*)$$$denotes a wavelet operator. A projection over convex sets (POCS) approach is conducted to solve the least-square reconstruction problem. After the soft-thresholding step at each iteration of L1-SPIRiT, we implement our feature refinement step as$$I_t=u+T\otimes v$$ where u is the denoised image, v is the residual image, $$$I_t$$$ is the feature refined image used to update the k-space, and T is the feature descriptor that can be regarded as a map or mask defining whether the pixel is located on the meaningful feature part. The feature descriptor is consisted of two parts: texture part $$$TT$$$ and structure part $$$TS$$$. The texture part $$$TT$$$ helps the descriptor handle the textures of high contrast, whereas the structure part $$$TS$$$ helps the descriptor preserve the structural architecture. For more details of the two parts of descriptor, please refer to Ref 6, 7. And to further enhance the effectiveness of our feature descriptor, we use S-shaped curve to fit $$$TT$$$ and $$$TS$$$. Finally, the proposed feature descriptor is defined as$$T=(TT+TS)/2$$ The value of each element in T is in the interval [0, 1], and for each pixel, the more its value is close to 1, the higher probability it belongs to the feature part. This descriptor can be seen as a filter or mask for preserving the meaningful feature information and discarding the noise and noise-like artifacts.

RESULTS

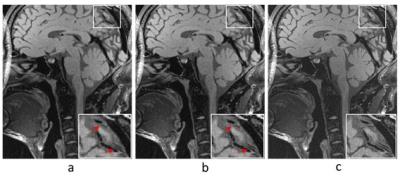
The 2D raw measurement data was obtained from a 3T scanner (SIEMENS MAGNETOM TrioTim) with 32-channel head coil by 3D SPACE sequence (TE/TR = 8.3/800ms, matrix=336×280), the spatial resolution is 0.64mm. The full k-space data was acquired and manually down-sampled to simulate a reduction factor of 7 using a Poisson disk sampling trajectory. The central 36*36 area was used for calibration. The prospective 4-fold 3D whole brain data was acquired on a healthy volunteer by 3D SPACE sequence (TE/TR = 4.8/800ms, matrix=320×320), the spatial resolution is 0.52mm. Informed consents were obtained before the examination. Fig.1 shows the reconstructions by L1-SPIRiT and the proposed feature refinement on the 2D data. It can be seen from the zoom-in images that the proposed strategy show better contrast than L1-SPIRiT in intracranial vessel wall exhibition. Fig.2 reveals the better performance of the feature refinement on the 3D whole brain reconstruction where we can see that feature refinement preserves the sharpness of the tissue and separates the vessel wall from surrounding tissues with clearer boundary than basic L1-SPIRiT.

CONCLUSION

The feature refinement strategy can effectively improve the sharpness and contrast of the intracranial artery vessel wall. Experiments on both 2D and 3D in vivo data demonstrate the superior performance of the proposed strategy in terms of image contrast improvement.

Acknowledgements

Grant support: China NSFC 61471350, the Natural Science Foundation of Guangdong 2015A020214019, the Basic Research Program of Shenzhen JCYJ20140610151856736 and US NIH R21EB020861 for Ying.