5178
The Signal-to-Noise Behavior of 3D SPIRiT Image Reconstruction1National Institutes of Health, Bethesda, MD, United States, 2Neurology, University of Pennsylvania, Philadelphia, PA, United States
Synopsis
Self-consistent parallel imaging (SPIRiT) is a self-calibrated, iterative parallel imaging technique that is not restricted by a particular k-space sampling pattern. 3D SPIRiT takes advantage of the 3D arrangement of a modern receive array to further improve image quality. Although SPIRiT was shown to yield higher image quality than does GRAPPA, especially at acceleration factors higher than 2, its signal-to-noise behavior has not been rigorously studied. In this study we investigate the image quality behavior of 3D SPIRiT and determine the optimal condition for best image quality.
Purpose
Modern RF coils often feature dense receive arrays aligned in all three spatial dimensions (1). Such arrangement stimulated the search and application of novel 3D-undersampled acquisition schemes in order to achieve higher acceleration factors for faster scanning with relatively less noise penalty (2-4). Accordingly, new reconstruction methods are being explored to optimize the image quality of such highly accelerated acquisitions. 3D self-consistent parallel imaging (SPIRiT) is an extension of the original SPIRiT method (5,6) that is uniquely suitable for 3D-accelerated acquisitions. SPIRiT is self-calibrated and allows flexible sampling in k-space. It is in principle simple to implement as only a single 3D kernel is required for the reconstruction of the entire 3D volume. As an iterative technique, SPIRiT was shown to yield improved image quality compared to the non-iterative method such as GRAPPA (7). However, SPIRiT is flexible and the optimization may not be straightforward. In this work we provide a detailed study on how the image quality varies in 3D SPIRiT in terms of image artifact and signal-to-noise ratio (SNR).Methods
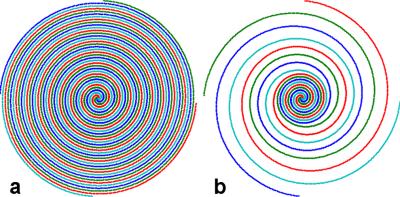
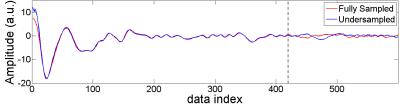
A fully-sampled brain volume was acquired with a stack-of-spirals trajectory in k-space at 3mm isotropic resolution and 216X216X144 mm3 FOV (Siemens Trio scanner, 3T, 32 channel head coil). The image volume was reconstructed with 2D NUFFT (8) and 1D FFT (in partition direction). To obtain 3D undersampled data, the volume was inversely gridded (8) back to an undersampled, variable-density k-space trajectory with inverse NUFFT, followed by inverse 1D FFT and partition undersampling. The variable-density spiral trajectory is fully sampled at 25% radius, 3X undersampled from 30% to 60%, and 5X undersampled beyond 65%. Sampling density varies linearly in the transition regions (from 25 to 30% and from 60 to 65%) (9). The fully- and under-sampled 2D spiral trajectories are shown in Fig. 1. The data along a representative spiral near the k-space center are shown in Fig. 2. For partition undersampling, the middle 13 partitions from 19 to 31 were kept intact, and 3X undersampled otherwise. The total undersampling factor was 5.5. For reconstruction, a 3D kernel of 5X5X3 was calibrated from the fully sampled center, and then conjugate-gradient (CG) was used for image calculation by imposing both kernel consistency and data consistency (5). Volumes were obtained at different numbers of iterations. Pseudo-multiple replica (PMR) (10) was used for signal-to-noise quantification by adding complex Gaussian noise to the original and undersampled data. 100 copies of such “noise-contaminated” data sets were generated and reconstructed.Results
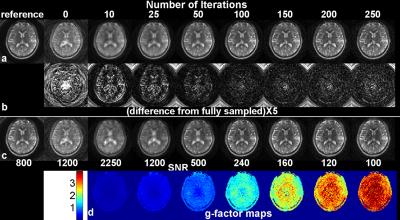
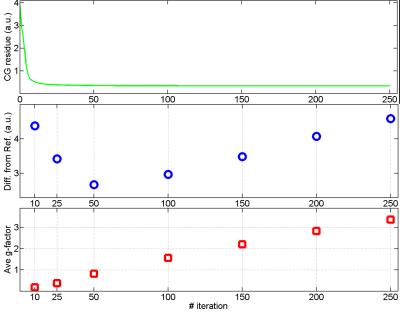
Figure 3 shows one representative slice of (a) the original and the 3D-SPIRiT volumes at different number of iterations, (b) the absolute difference from the reference volume multiplied by 5, (c) the empirical SNR maps, and (d) the empirical g-factor (11) maps. The numbers in (c) indicate the scales used for the corresponding maps to display all maps in similar brightness. Figure 3 reveals that as the number of iteration increases, the blurring artifact decreases, the empirical SNR decreases, and the empirical g-factor increases. Noticeably, in the presence of strong blurring artifact (10 and 25 iterations), the empirical g-factors are exceedingly low. The residue of the CG iteration, the total absolute difference across the entire volume, and the average g-factors are plotted in Fig 4 as functions of iteration number.Discussion
The results of this study have broad implications of parallel imaging in general. Apparently, the g-factor evolves with iteration in SPIRiT, which is in contrast to the non-iterative self-calibrated methods where the g-factor is solely determined by the kernel (12). For the range presented in this study, the g-factors show good linearity with iteration (Fig. 4). However, g-factor alone does not provide a good metric for image quality, especially when it appears to be too low, as demonstrated by Fig. 3 at 10 and 25 iterations where significant blurring artifacts exist. This suggests that the g-factor is a good metric of the image SNR only when artifacts are negligible. In our case, the best image quality was found between 50 and 100 iterations, which is much bigger than the number suggested for the 2D case (about 10 in Ref. (5)).Conclusion
In 3D SPIRiT image reconstruction of undersampled variable-density spiral data, strong blurring artifacts and deceivingly low g-factors co-exist without enough iteration (< 50). As more iterations are applied, both artifacts and empirical SNR are reduced. The best image quality is obtained between 50 and 100 iterations.Acknowledgements
No acknowledgement found.References
(1) Keil et al. A 64-channel 3T array coil for accelerated brain MRI, Magn Reson Med 70(2013):248
(2) Bilgic et al. Wave-CAIPI for highly accelerated 3D imaging, Magn Reson Med 73(2015):2152
(3) Deng et al. Rotated stack-of-spiral partial acquisition for rapid volumetric parallel MRI, Magn Reson Med 76(2016):127
(4) Chang et al. 3D-accelerated, stack-of-spirals acquisition and reconstruction of arterial spin labeling MRI, Magn Reson Med DOI:10.1002/mrm.26549
(5) Lustig et al. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space, Magn Reson Med 64(2010):457
(6) Shin et al. Rapid single-breath-hold 3D late gadolinium enhancement cardiac MRI using a stack-of-spirals acquisition, JMRI 40(2014):1496
(7) Griswold et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA), Magn Reson Med 47(2002):1202
(8) Fessler and Sutton, Nonuniform fast fourier transforms using min-max interpolation, IEEE-TSP 51(2003):560
(9) Lee et al. Fast 3D imaging using variable-density spiral trajectories, Magn Reson Med 50(2003):1276
(10) Robson et al. Comprehensive quantification of single-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions, Magn Reson Med 60(2008):895
(11) Pruessmann et al. SENSE: sensitivity encoding for fast MRI, Magn Reson Med 42(1999):952
(12) Breuer et al. General formulation for quantitative G-factor calculation in GRAPPA reconstruction, Magn Reson Med 62(2009):739
Figures