5171
Alias-reduced multicoil single-shot spatial temporally encoded MRI with referenceless sensitivity encoding1Center for Brain Imaging Science and Technology, Zhejiang University, Hangzhou, People's Republic of China, 2MR Collaboration Northeast Asia, Siemens Healthcare, Shanghai, People's Republic of China
Synopsis
Single-shot spatiotemporally encoded (SPEN) MRI is a novel fast imaging scheme with remarkably reduced geometric distortions at high field compared to conventional single-shot EPI. The k-space along SPEN dimension is undersampled, resulting in aliases at regions of rapid profile variation. The feasibility of utilizing sensitivity profiles of array receiver coils to unravel the undersampling aliases is investigated. High resolution relative sensitivity profiles can be obtained from multicoil 2D polynomial fitting of the SPEN reconstructed images without additional reference scans. The effectiveness of the SPEN SENSE strategy is validated by healthy human brain scans at 3T.
Purpose
Single-shot spatiotemporally encoded (SPEN) MRI is a novel fast imaging scheme with remarkably reduced geometric distortions at high field 1 compared to conventional single-shot EPI. The k-space along SPEN dimension is undersampled in order to obtain off-resonance immunity. Because different voxels along SPEN dimension are excited and refocused separately, the undersampling aliases can be highly reduced by reconstructing each voxel utilizing the signals around its refocusing echo 2. However, residual aliases still exist at regions of rapid profile variation where the aliased signals contain high spatial frequency components. With multicoil data acquisitions, the sensitivity profiles of array receiver coils are commonly used to unravel the undersampling aliases 3. In this study, the feasibility of combining SENSE with single-shot SPEN reconstruction is investigated.Methods
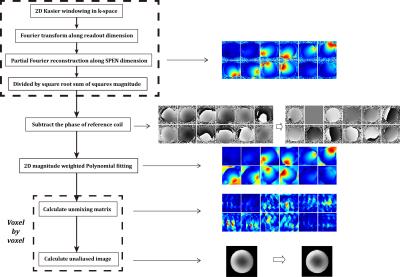
Healthy human brain data were acquired with informed consent on a SIEMENS 3T Prisma scanner using a 20-channel head coil (16 channels were activated for data collection), with the following parameters: field-of-view = 220x220mm2, slice thickness = 5mm, acquisition matrix size = 64x64, bandwidth and duration of the excitation chirp pulse = 50kHz and 5.12ms respectively (corresponding to fully-sampled points of 256 and acceleration factor of 4 along SPEN dimension), flip angle = 30°, acquisition bandwidth = 1502Hz/voxel, and TE = 66ms. Single-shot accelerated EPI data were also acquired with similar parameters and with 48 additional autocalibration data lines for comparison. The postprocessing procedures of the SPEN SENSE scheme are listed in Fig.1. Firstly, SPEN reconstructions were performed on each channel. Then high resolution relative sensitivity profiles 4 were obtained from multicoil SPEN reconstructed images directly, similar to the strategy implemented in multi-shot phase scrambling MRI 5. One coil was chosen as reference to remove the influence of rapid phase variations on sensitivity fitting. Next, SENSE unfolding was performed on multicoil SPEN reconstructed data of each voxel. Each voxel along SPEN dimension can be regarded as superposition of Nfull/N aliased voxels, each separated by N2/Nfull voxels, where N is the number of k-space points acquired and Nfull is the number of fully-sampled points. The SENSE equation set can be represented by
$$\bf {S}\bf{X}_\rm{unfold}=\bf{X}_\rm{pFT},\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{(1)}$$
where $$$\bf{S}$$$ is the complex sensitivity profile matrix, $$$\bf{X}_\rm{pFT}$$$ is the vector of multicoil voxel data obtained from partial Fourier reconstruction 2 and $$$\bf{X}_\rm{unfold}$$$ is the unfolded vector. This equation set can be easily solved by linear least squares estimation using
$$\bf{X}_\rm{unfold}=(\bf{S^H}\bf{\Psi}\rm^{-1}\bf{S}\rm)^{-1}\bf{S^H}\bf{\Psi}\rm^{-1}\bf{X}_\rm{pFT},\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{ }\text{(2)}$$
where $$$\bf{^H}$$$ represents transpose conjugate and $$$\bf{\Psi}$$$ is the noise covariance matrix. The aliased components are of large noise and discarded in this study. The unfolding calculations were performed voxel by voxel, instead of on each aliased group by conventional SENSE.
Results and discussion
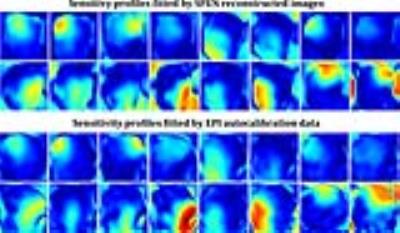
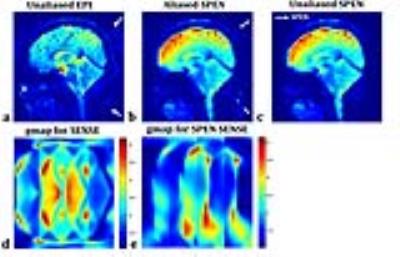
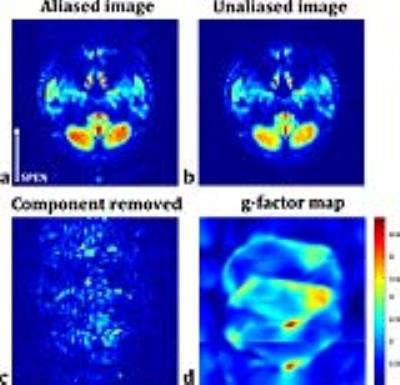
Two representative slices are selected for demonstration. One slice is on sagittal orientation with large signal-to-noise ratio. The sensitivity profiles respectively obtained from SPEN imaging data and the autocalibration data of conventional accelerated single-shot EPI are displayed in Fig.2 with similar distributions, demonstrating the influence of residual aliases after SPEN reconstruction to the accuracy of local coil sensitivities can be avoided by magnitude weighted 2D polynomial fitting. The unfolding result of SPEN SENSE is compared to that of conventional SENSE on EPI data in Fig.3. It can be seen that the aliased signals coming from the spine and the scalp are successfully removed with SPEN SENSE. Residual aliases still exist in conventional SENSE result because the limited spatial resolution of the autocalibration data results in local inaccuracy of the sensitivity profiles. Additionally, with SPEN SENSE the areas of larger g-factor values are more loosely distributed than with conventional SENSE, giving rise to higher SNR in most part of the FOV. The other slice for demonstration is on traversal orientation with lower overall SNR level shown in Fig.4. It can be seen that in the originally SPEN reconstructed image, undersampling aliases are quite obvious at two sides of the FOV along SPEN dimension, degrading the image quality. These aliases are mostly suppressed after SENSE unfolding. The g-factor values of cerebellum area are low, ensuring high SNR of the result.Conclusion
In this study, a reconstruction strategy based on multicoil sensitivity encoding is proposed for single-shot spatiotemporally encoded MRI. Experimental results demonstrate the effectiveness of the strategy in suppressing the undersampling aliases, even for slices with relatively lower SNR level. The strategy is potentially useful for BOLD and diffusion MRI applications in regions with severe susceptibility heterogeneities and difficult for routine EPI implementations.Acknowledgements
No acknowledgement found.References
1. Ben-Eliezer N, Irani M, Frydman L. Super-resolved spatially encoded single-scan 2D MRI. Magn Reson Med 2010; 63: 1594-1600.
2. Chen Y, Li J, Qu X, et al. Partial Fourier transform reconstruction for single-shot MRI with linear frequency-swept excitation. Magn Reson Med 2013; 69:1326-1336.
3. Pruessmann K P, Weiger M, Scheidegger M B, et al. SENSE: Sensitivity Encoding for Fast MRI. Magn Reson Med 1999; 42:952–962.
4. Bydder M, Larkman D J, Hajnal J V. Combination of Signals From Array Coils Using Image-Based Estimation of Coil Sensitivity Pro?les. Magn Reson Med 2002; 47:539–548
5. Zaitsev M, Schultz G, Hennig J, et al. Parallel Imaging with Phase Scrambling. Magn Reson Med 2015; 73:1407–1419.
Figures