5170
SPID Compressed Sensing for Parallel MRI: Flexible Sampling and Rapid Reconstruction1Biomedical Engineering Department, Technion - Israel Institute of Technology, Haifa, Israel, 2C.J. Gorter Center for High Field MRI Research, Department of Radiology, Leiden University, Leiden, TN, Netherlands
Synopsis
We introduce a new method combining Compressed Sensing (CS) and parallel MRI (pMRI) for fast MRI acquisition. The method, termed SPID-CS, is advantageous over existing methods since it (1) produces a high-quality initial reconstruction, (2) avoids aliasing related to sub-Nyquist sampling by joining information from different coils, (3) enables flexible k-space sampling, (4) converges much faster than conventional CS and (5) enables clinical real-time reconstruction due to its extremely short runtime.
Purpose
Compressed Sensing (CS) and parallel MRI (pMRI) are two powerful tools for fast MRI acquisition. However, methods attempting to combine them (e.g. [1-5]) face two main limitations. First, CS algorithms involve heavy computations and long run times which limit their clinical applicability [2]. Second, CS and pMRI have fundamentally contradicting sampling requirements: CS techniques require random k-space sampling [4] for effective incoherent artifacts removal. Parallel MRI methods, on the other hand, are often optimal for highly ordered (equi-spaced) k-space sampling [7]. In this work we introduce a new pMRI-CS reconstruction method based on the SPID (Sensitivity Profile Indexing and Deconvolution) pMRI technique [8]. The new method, referred to as SPID-CS, addresses the two above noted problems: it significantly reduces the number of CS iterations required to achieve a high-quality reconstruction, and it enables various and flexible sub-Nyquist k-space sampling schemes.Theory
SPID is a parallel-MRI non-iterative robust reconstruction method for sub-Nyquist k-space sampling, operating in a hybrid image-frequency domain. Uniquely, SPID produces the convolution of the unknown MR image $$$f(x,y)$$$ with a known user-defined kernel $$$g(x)$$$. The resulting convolution image $$$h(x,y)$$$ is computed in a 1D manner for each row of $$$f(x,y)$$$ separately, in the image domain, i.e. for row $$$y0$$$: $$$h(x,y0)=f(x,y0)*g(x)$$$. Once this convolved image is generated, $$$f(x,y)$$$ is simply calculated by applying a 1D deconvolution procedure. The proposed SPID-CS method involves two steps: (1) SPID reconstruction from k-space samples, and (2) CS reconstruction initiated from the SPID result. This process is general and suitable for any sub-Nyquist k-space sampling comprising of a set of columns or rows. The set can be obtained using flexible acquisition schemes including ordered, varying-period and random sampling.Methods
A T1-weighted scan was performed on a healthy volunteer on a Phillips 7T scanner equipped with a 32-channel head-coil using a gradient echo protocol. Full k-space was acquired and then decimated offline. Sensitivity maps were computed from separate low-resolution scans. Post-processing was performed in MatLab on an 8 core Intel 3.6 GHz PC (16 GB RAM). SPID [8] was implemented with a Gaussian kernel ($$$sigma=1$$$) and a standard frequency-domain deconvolution. A POCS-based CS reconstruction was implemented with the Stationary Wavelet Transform (SWT) [9], using a Daubechies-2 wavelet and soft thresholding. For comparison with the proposed method we also computed the conventional POCS-based CS reconstruction, which is initiated from a Zero-Filled (ZF) undersampled k-space, termed herein as ZF-CS. All reconstruction qualities were evaluated by their correlation with a gold standard image calculated from the full k-space according to the method proposed by Roemer et al. [10].Results & Discussion
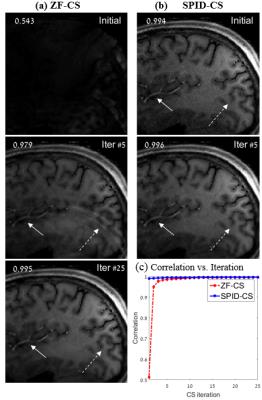
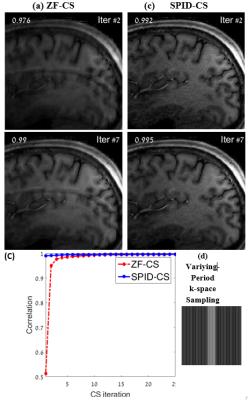
Fig. 1 shows images reconstructed from a regularly (equi-spaced) sampled k-space with a reduction factor of $$$R=4$$$. The SPID-CS initial reconstruction is clearly superior to the standard ZF-CS one; SPID produced an image without the aliasing present in the ZF-CS reconstruction (see arrows). The SPID-related noise was removed by the CS process within 5 iterations, whereas the standard ZF-CS required 25 iterations to reach the same quality. The faster convergence of SPID-CS is also evident from the comparison of the SPID-CS and ZF-CS correlation curves depicted in Fig. 1c. Fig. 2 shows similar results for reconstructions from k-space samples obtained using a varying-period sampling with $$$R=4$$$ (shown in Fig 2d).
Another advantage of SPID-CS is that the heaviest SPID computations are performed offline, prior to the MRI acquisition, and only once for all slices. In this work they consumed 60.8 seconds. In the post-processing stage, SPID-CS reconstruction is highly efficient: it required only 0.75 seconds until convergence, whereas the ZF-CS reconstruction required 9.09 seconds (convergence was arbitrarily defined when the correlation reached 0.995). Further improvement of the SPID computation may be obtained by parallelizing the process; this is attainable since SPID operates on each row of $$$h(x,y)$$$ separately.
Conclusion
We introduced the SPID-CS method which (1) produces a high-quality initial reconstruction, (2) avoids aliasing related to sub-Nyquist sampling by joining information from different coils, (3) enables flexible k-space sampling, (4) converges much faster than conventional CS and (5) enables clinical real-time reconstruction due to its extremely short runtime.Acknowledgements
No acknowledgement found.References
1. Murphy, Mark, et al. "Fast-SPIRiT compressed sensing parallel imaging MRI: scalable parallel implementation and clinically feasible runtime." IEEE transactions on medical imaging 31.6 (2012): 1250-1262.
2. Liang, Dong, et al. "Accelerating SENSE using compressed sensing." Magnetic Resonance in Medicine 62.6 (2009): 1574-1584.
3. Wu, Bing, et al. "Prior estimate-based compressed sensing in parallel MRI." Magnetic resonance in medicine 65.1 (2011): 83-95.
4. Liu, Bo, Yi Ming Zou, and Leslie Ying. "SparseSENSE: application of compressed sensing in parallel MRI." 2008 International Conference on Information Technology and Applications in Biomedicine. IEEE, 2008.
5. Otazo, Ricardo, et al. "Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI." Magnetic Resonance in Medicine 64.3 (2010): 767-776.
6. Feng, Li, et al. "Golden-angle radial sparse parallel MRI: Combination of compressed sensing, parallel imaging, and golden-angle radial sampling for fast and flexible dynamic volumetric MRI." Magnetic resonance in medicine 72.3 (2014): 707-717.
7. Pruessmann, Klaas P., et al. "SENSE: sensitivity encoding for fast MRI." Magnetic resonance in medicine 42.5 (1999): 952-962.
8. Azhari, Haim, Daniel K. Sodickson, and Robert R. Edelman. "Rapid MR imaging by sensitivity profile indexing and deconvolution reconstruction (SPID)." Magnetic resonance imaging 21.6 (2003): 575-584.
9. Kayvanrad, Mohammad H., et al. "Stationary wavelet transform for under-sampled MRI reconstruction." Magnetic resonance imaging 32.
10 (2014): 1353-1364. 10. Roemer, Peter B., et al. "The NMR phased array." Magnetic resonance in medicine 16.2 (1990): 192-225.