5166
Nonlinear SPIRiT using a second order virtual coil for improved parallel imaging reconstruction1Shenzhen Institutes of Advanced Technology, Shenzhen, People's Republic of China, 2The state University of New York (SUNY) at Buffalo, United States
Synopsis
The nonlinear relationship between missing and acquired data in k-space has been proved in nonlinear GRAPPA. In this work, we propose nonlinear SPIRiT which integrates the polynomial kernel method into SPIRiT via a simple second-order virtual coil approach. The proposed method represents the relationship between missing and acquired data in k-space of SPIRiT using a more accurate nonlinear model. In vivo results demonstrated that nonlinear SPIRiT could suppress aliasing artifact or noise better than SPIRiT, and was applicable to more acceleration scenarios than nonlinear GRAPPA.
Introduction
Nonlinear GRAPPA using kernel method improves the reconstruction quality of popular GRAPPA 1 at high outer reduction factor 2 via representing the relationship between missing and acquired k-space data into a nonlinear model. However, nonlinear GRAPPA reconstruction requires much more calibration data than GRAPPA to fit out the nonlinear model 3, and this severely limits its application in scenarios where calibration data is limited such as 2D acceleration in 3D imaging. This work aims to integrate the benefits of nonlinear model into SPIRiT 4 through an intuitive second order virtual coil approach 5 to improve SPIRiT reconstruction and to overcome the limitations of nonlinear GRAPPA.Method
Theory The kernel methods in
machine learning are typically used to find nonlinear relationships in dataset
via transforming the data to a new feature space. This work aims to employ the
kernel methods into SPIRiT to extract the intrinsic nonlinear relationship between
data and its neighbors in k-space. The proposed nonlinear SPIRiT contains three
steps. Firstly, both the calibration and subsampled data are transformed into a
higher dimensional space via kernel methods. Polynomial kernel is employed as
it has explicit representation, and includes the linear relationship as a
special case. A two order polynomial kernel uses the original data and the
square of data as the first and second-order terms separately. The virtual coil
concept is employed to simplify the implementation. A new k-space data is
generated with the channel number being doubled. The data in physical coils is
kept as the first-order terms, while the virtual coils containing the square of
original data point-by-point works as the second-order terms. Secondly, the
least-squares method used by original SPIRiT calibration is still used to
estimate the nonlinear relationship from the transformed data. Finally, the
nonlinear model is applied on the physical and virtual coil data in a POCS
iteration to recovery unacquired data.
Experiment
Fully
sampled 3D brain data with elliptical scanning was acquired from a healthy
volunteer using a T1 weighted SPACE sequence and a 32 channel coil set on a 3T
Siemens Tim Trio MRI system. Informed consents were obtained before the
examination. A ky-kz slice was extracted after 1D Fourier Transform along
readout direction. The 2D full k-space data was compressed to 18 channels for
efficient computation. Imaging parameters were: FOV = 215x179x133 mm3, matrix
size = 336x280x208, and isotropic resolution of 0.64 mm. Firstly, 1D uniform
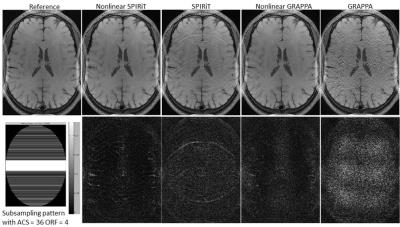
subsampling with an outer reduction factor of 4 and embedded 36 calibration
lines were simulated to compare nonlinear SPIRiT with nonlinear GRAPPA, as well
as GRAPPA and SPIRiT. Both linear and nonlinear SPIRiT were solved by POCS
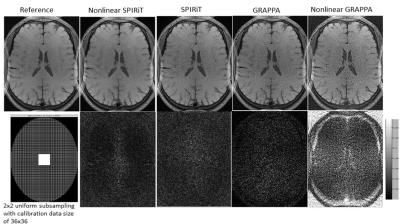
algorithm using 30 iterations. Secondly, a 2D uniform subsampling with both
acceleration factors being 2 and calibration data size of 36x36 was simulated
to investigate the performance of nonlinear SPIRiT with 2D acceleration and compared with nonlinear GRAPPA.
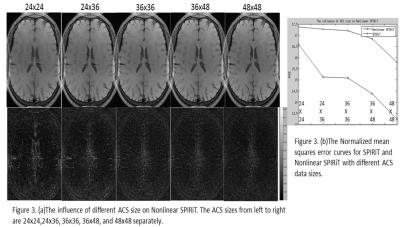
Finally, the influence of the amount of calibration data on the reconstruction
quality of nonlinear SPIRiT was investigated with a uniform 2x2 subsampling and
compared with SPIRiT reconstruction.
Results
The comparison of nonlinear SPIRiT with SPIRiT, GRAPPA and nonlinear GRAPPA was illustrated in Figure 1. Nonlinear SPIRiT suppressed the amplified noise better than nonlinear GRAPPA, and largely removed the residual aliasing artifacts in SPIRiT reconstruction which suffered from highly accelerated uniform subsampling. Figure 2 demonstrated the nonlinear SPIRiT reconstruction for 2D accelerated data. Nonlinear SPIRiT suppressed the noise better than GRAPPA and SPIRiT. However with the same calibration data, nonlinear GRAPPA was unable to fit out GRAPPA weights due to insufficient ACS data and suffered obvious artifacts. Figure 3(a) illustrated reconstructed images and corresponding difference images for the 2x2 accelerated data with different sizes of calibration data, and Figure 3(b) plotted the normalized mean squared errors. The sizes of calibration data were 24x24, 24x36, 36x36, 36x48 and 48x48 separately, and all calibration data were used in subsequent POCS reconstruction. The result demonstrated the noise suppression performance of nonlinear SPIRiT was not significantly dependent on the size of calibration data, and a calibration data size of 36x36 was enough.Discussion and Conclusion
The polynomial kernel method was integrated into SPIRiT via a virtual coil approach to better model the nonlinear relationship between missing and acquired data in k-space. In vivo result demonstrated nonlinear SPIRiT suppressed noise or residual aliasing artifacts better than SPIRiT and was more applicable to different acceleration scenarios comparing with nonlinear GRAPPA. Further work needs to investigate method of better balancing the blurring and noise suppression effects, and improves the noise behavior of nonlinear SPIRiT reconstruction.Acknowledgements
Grant support: China NSFC 61471350, the Natural Science Foundation of Guangdong 2015A020214019, the Basic Research Program of Shenzhen JCYJ20140610151856736 and US NIH R21EB020861 for Ying.References
1. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, and Haase A. A Generalized autocalibrating partially parallel acquisition (GRAPPA). Magnetic Resonance in Medicine, 2002; 47:1202-1210.
2. Madhusoodhanan S and Paul JS. A quantitative survey of GRAPPA reconstruction in parallel MRI: impact on noise reduction and aliasing. Concepts Magn Reson Part A, 2006; 1-19.
3. Chang Y, Liang D, and Ying L. Nonlinear GRAPPA: A Kernel Approach to Parallel MRI Reconstruction. Magnetic Resonance in Medicine, 2012; 68:730-740.
4. Lustig M and Pauly JM. SPIRiT: Iterative Self-consistent Parallel Imaging Reconstruction From Arbitrary k-Space. Magnetic Resonance in Medicine, 2010; 64:457-471.
5. Blaimer M, Gutberlet M, Kellman P, Breuer FA, Kostler H, and Griswold MA. Virtual Coil Concept for Improved Parallel MRI Employing Conjugate Symmetric Signals. Magnetic Resonance in Medicien, 2009; 61:93-102.
Figures