5163
Improved Parallel Imaging with Resilience to Gradient Errors1Radiology and Biomedical Imaging, Yale University, New Haven, CT, United States, 2Biomedical Engineering, Yale University, New Haven, CT, United States
Synopsis
FRONSAC encoding, which adds a rapidly oscillating low-amplitude nonlinear gradient to a standard undersampled trajectory based on linear gradients, has been shown to significantly improve k-space coverage and parallel imaging reconstructions. This abstract further shows that a fixed FRONSAC waveform improves image quality for Cartesian trajectories of various FOV and resolution, while avoiding many of the pitfalls of other highly efficient gradient trajectories. Results show that FRONSAC provides better reconstruction than Cartesian encoding alone, while offering better resilience to delays and off-resonance effects than non-Cartesian trajectories, such as spiral.
Introduction
One of the attractive features of Cartesian imaging is that experimental imperfections, e.g. gradient delays, trajectory errors, or off-resonance spins, lead to relatively simple errors in the reconstructed image. But Cartesian encoding is not optimal for undersampled parallel imaging.1 Non-Cartesian trajectories, such as spiral, permit higher undersampling factors, but these methods are generally intolerant of experimental imperfections and require rigorous field mapping. Since each new FOV, matrix resolution or slice orientation requires a different gradient trajectory, measuring or predicting these trajectories is a significant challenge.2
With FRONSAC encoding, the readout is accompanied by two oscillating nonlinear gradients, which produce a rotating nonlinear field. (Figure 1) Cartesian imaging with FRONSAC encoding is a recent method which enhances the k-space coverage of parallel imaging and results in better undersampled images, while avoiding many pitfalls of other highly efficient gradient trajectories.3,4 This work considers adding a fixed FRONSAC encoding field to Cartesian acquisitions where the linear gradients are adjusted to image different FOVs and matrix sizes, and various experimental imperfections are introduced. Results show that FRONSAC provides markedly better images than Cartesian encoding alone, while offering better resilience to delays and off-resonance than non-Cartesian trajectories, such as spiral.
Methods
All simulations were performed in MATLAB (The MathWorks, Natick, MA) using measured coil profiles from an 8-channel array and Kaczmarz reconstruction. All trajectories were 2-fold oversampled in the readout direction, with matrix size of 96 and FOV=20cm except where otherwise stated. Undersampling in Cartesian and FRONSAC trajectories was performed on Nyquist sampled trajectories in the phase encode direction. Spiral trajectories used a uniform spiral with a number of turns equal to either 1/4 or 1/8 of the matrix resolution. FRONSAC gradients were simulated with a cosine waveform on the C2 channel (G(x,y)=x2+y2) and sine waveform on the S2 channel (G(x,y)=2xy) with amplitude 120Hz/cm2 and frequency 1.7kHz over a 12ms readout window. FOV was varied bychanging the amplitude of the linear gradients as well as the size of the phantom, and spatial resolution was varied by effectively adjusting amplitude of linear gradients and sampling rate. Experimental imperfections were simulated by modifying the encoding used to generate data while using the ideal encoding in the reconstruction matrix. Gradient delays were simulated using a linear approximation between the nominal k-space point and the previous k-space point. Delays on the Gx channel are those listed on the figure while Gy used a delay equal to half that value. Off-resonance behavior was simulated by adding linear gradients across the FOV with bandwidth as noted. A small amount of white Gaussian noise was added to each signal such that the SNR of a fully sampled Cartesian image is 500.Results
Figure 2 compares undersampled images from Cartesian, spiral, and FRONSAC encodings assuming perfectly known gradient encodings. Highly undersampled Cartesian images show pronounced artifacts which are removed by the additional FRONSAC encoding. Figure 3 shows that a fixed FRONSAC waveform can be used to improve reconstruction despite changes to the Cartesian trajectory which allow for different FOV and resolution. Therefore, FRONSAC gradients do not need to be tailored to the scan prescription to improve parallel imaging performance; a single well-characterized FRONSAC waveform can be applied to improve a range of scan prescriptions. Figure 4 compares R=8 images with a linear off-resonance error and demonstrates that FRONSAC imaging, like Cartesian, is less sensitive to this error, while still reducing undersampling artifact. Figure 5 makes a similar comparison for various delays in the linear gradients.Discussion
FRONSAC encoding improves upon the undersampling limitations of Cartesian imaging and the trajectory mapping requirements of non-Cartesian imaging. Because most of the encoding is performed by the linear gradients, Cartesian FRONSAC retains many desirable features of Cartesian imaging, such as simpler artifacts in the presence of experimental imperfections. Other simulations (not shown) suggest that the FRONSAC encoding itself must be known to high accuracy. However, since a single FRONSAC waveform can be used (Figure 3), high quality empirical field mapping of a single trajectory can improve a wide range of scan prescriptions.5-7Conclusion
The addition of FRONSAC encoding to Cartesian trajectories can improve the ability to undersample images without sacrificing tolerance to experimental imperfections.Acknowledgements
Authors gratefully acknowledge support from 1K01CA168977.References
[1] Wright et al, JMRI 2014. [2] Delattre et al, MRI 2010. [3] Wang et al, MRM 2015. [4] Luedicke et al, ISMRM 2016. [5] DeZanche et al, MRM 2008. [6] Testud et al, MRM 2015. [7] Stockmann et al, MRM 2010.Figures

Figure1: FRONSAC Pulse Sequence
Cartesian FRONSAC encoding adds an additional oscillating gradient to a standard spin warp sequence. This amounts to adding a rotating nonlinear field to the readout, which spreads k-space sampling and improves images from undersampled scans.
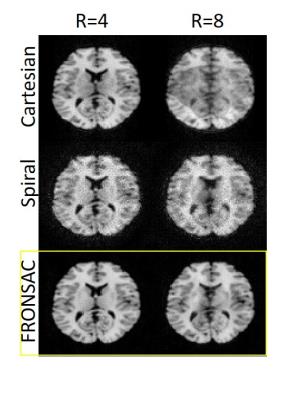
Figure 2: Undersampled Images
FRONSAC improves images from undersampled trajectories. Rows compare Cartesian with 12 or 24 readouts, spiral trajectories with 12 or 24 rotations in k-space, and FRONSAC with 12 or 24 readouts. FRONSAC encoding is identical to the Cartesian case, except that an additional rapidly rotating nonlinear gradient is played with each readout.
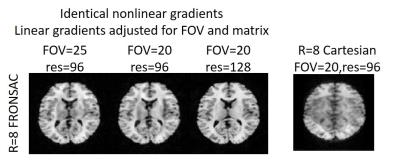
Figure 3: A Fixed FRONSAC Waveform Can Enhance Many Scans
These images show that the FRONSAC gradients do not need to be tailored to the scan prescription to improve parallel imaging performance. A single well-characterized FRONSAC waveform can dramatically improve images despite changes to the linear sampling pattern, such as those needed to change FOV or resolution.
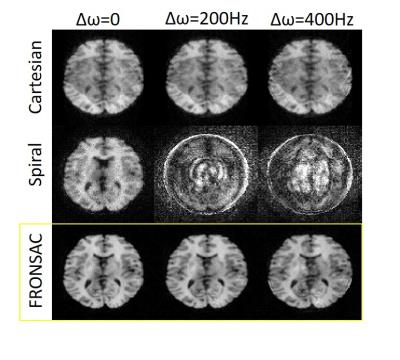
Figure 4: Sensitivity to Off-Resonance Spins
FRONSAC is insensitive to off-resonance imperfections. R=8 imaging was simulated with various linear off-resonance for three sequences: Cartesian with 12 phase encode steps, spiral with 12 cycles, and FRONSAC with 12 phase encode steps. Cartesian images show strong undersampling artifacts at this high acceleration, but linear off-resonance generates simple distortions that further degrade the parallel imaging only slightly. In a perfectly shimmed field, the spiral and FRONSAC images are of comparable quality and quite good, but FRONSAC reconstructions do much better in the presence of off-resonance.
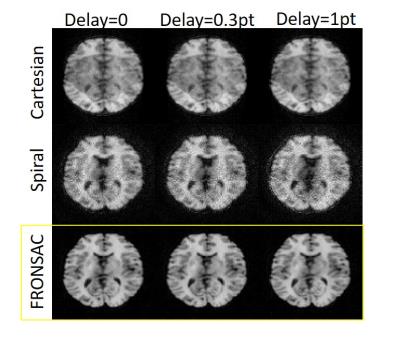
Figure 5: Sensitivity to Gradient Delays
FRONSAC is insensitive to gradient delays. Since FRONSAC is based on a Cartesian trajectory along the linear gradients, it shows similar insensitivity to delays in those channels. As in a Cartesian image, the error in the encoding matrix is equivalent to adding a fixed phase roll to the reconstructed object, which does not affect the magnitude image.