Synopsis

We propose an extension to Regularized Non-Linear Inversion (NLINV), which simultaneously reconstructs multiple images and sets of coil sensitivity profiles. This method, termed ENLIVE (Extended Non-Linear InVersion inspired by ESPIRiT), can be related to a convex relaxation of the NLINV problem subject to a low-rank constraint. From NLINV, it inherits its suitability for calibrationless and non-Cartesian imaging; from ESPIRiT it inherits robustness to data inconsistencies.

Introduction

Recently, ESPIRiT[1] has been shown to provide GRAPPA[2]-like robustness towards data inconsistencies. In particular, in cases where the chosen FOV is smaller than the object, traditional SENSE[3]-like methods that only use a single set of coil sensitivity profiles exhibit artifacts[4]. In ESPIRiT, robust reconstruction is possible through a relaxed SENSE-model which uses multiple sets of coil sensitivity profiles.

We propose an extension to Regularized Non-Linear Inversion (NLINV)[5], which simultaneously reconstructs multiple images and sets of coil sensitivity profiles. This method, termed ENLIVE (Extended Non-Linear InVersion inspired by ESPIRiT), can be related to a convex relaxation of the NLINV problem subject to a low-rank constraint. From NLINV, it inherits its suitability for calibrationless and non-Cartesian imaging; from ESPIRiT it inherits robustness to data inconsistencies.

Theory

Algorithm ENLIVE is based on the non-linear optimization problem: $$\underset{m^i,c_j^i}{\mathrm{arg\,min}} \sum_j \|y_j - \mathcal{PF}\{\sum_i^kc^i_jm^i\}\|^2_2 + \frac{\alpha}{2}\sum_{i,j}(\|Wc^i_j\|_2^2 + \|m^i\|_2^2)$$ where $$$y_j$$$ is data collected by the $$$j$$$th coil, $$$c_j^i$$$ and $$$m^i$$$ are $$$k$$$ sets of unknown coil sensitivity profiles and unknown images, $$$\mathcal{F}$$$ the discrete Fourier transform, $$$\mathcal{P}$$$ the projection onto the measured k-space positions and $$$W$$$ a weighting matrix penalizing high frequencies in the coil profiles. With one map ($$$k=1$$$), this is exactly the NLINV problem. This optimization problem is solved using the iteratively regularized Gauss-Newton method.

Since this problem is symmetric in the maps, we require the $$$k$$$ sets of coil profiles to be orthogonal, breaking the symmetry using Gram-Schmidt orthogonalization after each Newton step.

Low-rank constraint As explained in the following, this quadratically regularized bilinear optimization problem corresponds to a convex formulation using nuclear-norm regularization. Although this is not used for computation, it explains why ENLIVE produces low-rank solutions that automatically only use the required number of maps.

NLINV ($$$k=1$$$) can also be understood as blind multi-channel deconvolution in k-space. As shown previously[6], blind deconvolution can be lifted into a convex problem in terms of a matrix $$$X=UV^T$$$, where $$$U\in\mathcal{C}^{N\times k}$$$ is formed by $$$k$$$ vectorized images $$$m^i$$$ of length $$$N$$$ and $$$V\in\mathcal{C}^{M\times k}$$$ is formed by stacking the weighted coil sensitivity profiles $$$Wc_j^i$$$ to a vector of length $$$M$$$. Together with a linear operator $$$\mathcal{A}_j$$$ which maps $$$UV^T$$$ onto $$$\mathcal{PF}\{\sum_i^kc^i_jm^i\}$$$, this leads to a fully convex formulation: $$\underset{X}{\mathrm{arg\,min}} \sum_j\|y_j-\mathcal{A}_j\{X\}\|^2_2 + \alpha\|X\|_\star$$ where $$$\|\mathord{\cdot}\|_\star$$$ is the nuclear norm. Ahmed et al.[6] have shown that if this problem has a solution of rank $$$< k$$$, then the solution corresponds to the solution of the original deconvolution problem.

Methods

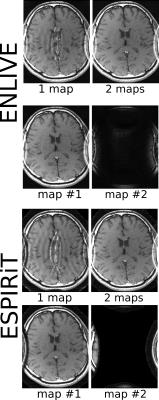
We applied ENLIVE to the same dataset used in [1], a retrospectively 2-fold undersampled 2D spin-echo dataset (TR/TE=550/14 ms, FA=90°, BW=19 kHz, matrix size: 320x168, slice thickness: 3 mm, 24x24 calibration region) with an FOV of 200 x 150 mm², acquired at 1.5 T using an 8-channel coil. This FOV is smaller than the head of the subject in the lateral direction which lead to artifacts in traditional SENSE reconstruction. These data were then reconstructed using ENLIVE allowing 1 or 2 maps; and with ESPIRiT using 1 or 2 maps.

To show the possibility of calibrationless imaging, a fully-sampled 3D FLASH dataset (TR/TE=20/4.9 ms, FA=40°, BW=34.2 kHz, matrix size: 160x112x160, Resolution: 1x1x1.1 mm³) of a custom-build phantom was acquired at 3 T using a 20-channel head coil. Here, too, the FOV is smaller than the phantom. A single slice along the readout direction was selected and retrospectively undersampled using a Poisson-disc sampling pattern with acceleration of 2 and without calibration region. Reconstructions were performed using ENLIVE allowing 1 or 2 maps and with SAKE[7]. Reconstruction time using a single CPU was 6.4 s for ENLIVE and 3494 s for SAKE.

The proposed method was implemented in the BART[8] and existing ESPIRiT and SAKE implementations from BART were used.

Results

ENLIVE allowing multiple maps enables artifact-free reconstruction (Figure 1) even in the case of an FOV smaller than the object, which is not the case when using a single map. Allowing 2 maps, he reconstruction quality of ENLIVE is comparable to ESPIRiT using 2 maps; both methods eliminate the central artifacts.

When using Poisson-disc sampling (Figure 2), ESPIRiT is no longer applicable. Here, too, ENLIVE with only 1 map shows artifacts, which are eliminated by allowing 2 maps. SAKE, too, provides artifact free reconstruction, albeit with significantly longer reconstruction time.

Conclusion

Acknowledgements

References

[1]: M. Uecker et al., MRM 71:990-1001 (2014).

[2]: M. A. Griswold et al., MRM 47:1202-1210 (2002).

[3]: K. P. Pruessmann et al., MRM 42:952-962 (1999).

[4]: M. A. Griswold et al., MRM 52:1118-1126 (2004).

[5]: M. Uecker et al., MRM 60:674-682 (2008).

[6]: A. Ahmed et al., IEEE Trans. Inform. Theory 60:1711-1732 (2014).

[7]: P. J. Shin et al., MRM 72:959-970 (2014).[8]: M. Uecker et al., ISMRM 23:2486 (2015).