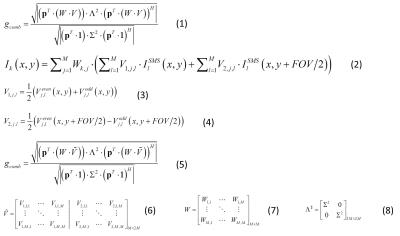5159

Analytical G-factor Calculation for Slice-GRAPPA with Dual “Even-Odd” Kernels (SG-DK)
Haifeng Wang1,2, Jonathan R. Polimeni1,2,3, Berkin Bilgic1,2, Lawrence L. Wald 1,2,3, and Kawin Setsompop1,2

1Massachusetts General Hospital, Boston, MA, United States, 2Harvard Medical School, Boston, MA, United States, 3Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, United States

Synopsis

Slice-GRAPPA (SG) is often used to reconstruct blipped-CAIPI simultaneous multi-slice EPI data, in particular in conjunction with the dual even-odd kernel approach (SG-DK) to mitigate ghosting related reconstruction artifacts. To achieve good performance in blipped-CAIPI acquisition, the CAIPI shift factor should be optimized in a case by case manner to minimize g-factor penalty. The g-factor is influenced by the reconstruction approach and so far a fast analytical g-factor calculation has been developed only for standard SG reconstruction but not SG-DK, where time-consuming Monte Carlo simulation is still needed. Here we propose an analytical g-factor calculation for SG-DK and demonstrate that the proposed method is fast and accurate. Our simulation and experimental results also highlight the superior performance of SG-DK over SG reconstruction, both in mitigating image artifacts and noise penalty.

INTRODUCTION

Blipped-CAIPI SMS-EPI 1-4 has been widely used for diffusion and fMRI acquisitions, in particular in conjunction with the dual kernel Slice-GRAPPA (SG-DK) reconstruction. The dual-kernel approach is attractive because of its robust image unaliasing performance in the present of N/2 ghost. This is achieved through the utilization of a different slice-GRAPPA kernel for the odd and even k-space lines. In order to achieve optimal performance in blipped-CAIPI SMS-EPI, the CAIPI shift factor should be optimized in a case-by-case manner to minimize the g-factor noise penalty. The g-factor is influenced by the reconstruction approach and a fast analytical g-factor calculation has been developed for standard SG and other reconstruction approaches 5,6. However, for SG-DK, time-consuming Monte Carlo simulation 7 is still needed to obtain g-factor maps. Here we extend the standard analytical g-factor calculation to allow it to be compatible with the dual kernel SG (SG-DK) reconstruction. We demonstrate such approach is fast and accurate; with the resulting simulation and experiment highlighting the superior performance of SG-DK over standard SG reconstruction, both in mitigating image artifacts and noise penalty.

THEORY

The standard analytical g-factor calculation 5 for acquisitions that contains both slice and in-plane accelerations (MB x Rinplane), reconstructed using SG and in-plane GRAPPA is shown as equation 1 in table 1. Here, p represents the coil sensitivities, and W and V the in-plane and slice GRAPPA weights in image domain. Equation 2 shows the image domain reconstruction equation for kth coil image (Ik) for the case where SG-DK and in-plane GRAPPA are utilized. Here, V1 and V2 represent modified image domain slice-GRAPPA weights, synthesized from the odd and even GRAPPA kernel weights (Veven and Vodd) according to equations 3 and 4. Equation 5 shows the analytical g-factor formulation for the combined SG-DK and in-plane GRAPPA reconstruction, where the slice weight V is replaced by Ṽ that is a hybrid slice weight combined from the odd and even kernels, Veven and Vodd (as per equation 6). Here, V1,j,l and V2,j,l are separately computed as the sum of odd-even weights and the difference of odd-even weights in image domain; Σ² is the noise covariance matrix; Λ² is the augmented noise covariance matrix from Σ².

METHODS

In vivo human brain data were acquired using the blipped-CAIPI SMS-EPI sequence (TE/TR: 74/3600ms; matrix: 297×147×91; voxel size: 1.5mm iso; FOV: 220mm; MB × Rinplane = 3×3; FOV/2 CAIPI shift) on a SIEMENS 3T Prisma scanner (SIEMENS, Erlangen, Germany) with commercial 64-channel head/neck coil (12 neck channels were not used during acquisition). Fully sampled dataset with matching image distortion was also obtained as references scan, using multi-shot EPI acquisition. This fully sampled reference dataset was used for g-factor calculations to compare the Monte Carlo and the proposed analytical method. Two acceleration factors were simulated at MB × Rinplane = 3×2 and 3×3, with the later matching that of the acquired accelerated dataset. To carefully replicate the situation in the slice-accelerated acquisitions, only “slice-averaged” ghost correction is performed on the simulated accelerated data prior to slice unaliasing via SG/SG-DK. Additional g-factor simulations and image reconstructions were also performed for an exaggerated ghost case (6 times of actual ghost level) to mimic acquisition scenario that contain high ghost levels. Here, ghost was added to the dataset prior to SG/SG-DK reconstruction. All image reconstruction and analysis were performed offline in MATLAB.

RESULTS

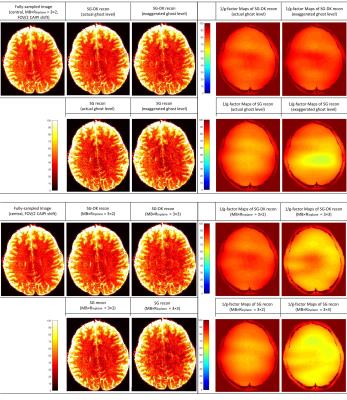
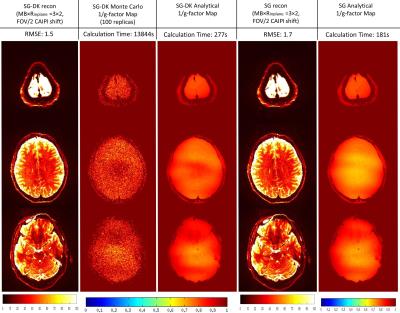
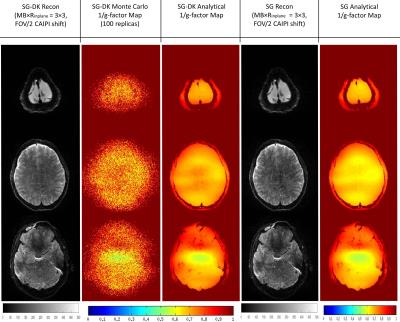
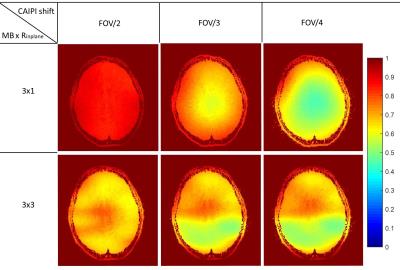
In the simulations of Figure 1, the reconstructed images from SG and SG-DK were compared at different accelerations (MB × Rinplane = 3 × 2 and 3 × 3) and different EPI ghost levels. The results show SG-DK can provide improved reconstruction and lower noise penalty when compared to SG reconstruction, particularly when the ghost level is high. In Figure 2 and 3, the simulation (MB × Rinplane = 3 × 2; FOV/2 CAIPI shifting) and in vivo experiment (MB × Rinplane = 3 × 3; FOV/2 CAIPI shifting) illustrate the proposed g-factor calculation provide similar results to the traditional Monte Carlo method (100 replicas). Moreover, the calculation time of the analytical method was 50× less than the traditional method. Figure 4 shows the analytical method could be used to quickly analyze the SNR performance at different accelerations (MB × Rinplane = 3×1 and 3×3) and CAIPI shift (FOV/2, FOV/3 and FOV/4).

CONCLUSION

SG-DK reconstruction results in less noise enhancements and image artifacts than SG reconstruction. The proposed analytical g-factor calculation of SG-DK is accurate and much faster than the traditional Monte Carlo method. This should aid in the analysis of the SNR performance and in the optimization of sequence parameters.

Acknowledgements

NIH NIBIB R01-EB019437 and NIH Shared Instrument Grant S10RR023043

References

1. Setsompop K, et. al. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn Reson Med. 2012; 67(5):1210-24.

2. Breuer FA, et. al. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med. 2005; 53(3):684-91.

3. Setsompop K, et. al. Improving diffusion MRI using simultaneous multi-slice echo planar imaging. Neuroimage. 2012; 63(1):569-80.

4. Cauley SF. et. al. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn Reson Med. 2014; 72(1):93-102.

5. Breuer FA, et. al. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn Reson Med. 2009; 62(3):739-46.

6. Zhu K, et. al. Analytical G-factor for Cartesian Simultaneous Multi-Slice Imaging. ISMRM 2016. Abstract: 609.

7. Robson PM, et. al. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magn Reson Med. 2008; 60(4):895-907.

Figures

Table1: analytical g-factor calculation equations

Figure 1. Image reconstructions and analytical 1/g factor maps of the synthesized accelerated acquisitions at two different acceleration factors (MB × Rinplane = 3 × 2 and 3 × 3) and at two different ghost levels (i) actual ghost level and (ii) exaggerated ghost level (6 times of actual ghost level). All acquisitions ultilizes the same FOV/2 CAIPI shift. Image reconstruction from SG-DK and SG are shown along with analytical 1/g-factor maps for SG-DK and SG. In all cases, the results from the central reconstructed slice are shown, which demonstrates the superior performance of SG-DK, particularly in the case of exaggerated ghost level.

Figure 2. Comparisons of 1/g-factor maps from the Monte Carlo method for SG-DK, and from the analytical approach for SG-DK and SG reconstructions, along with the image reconstruction results (of synthesized accelerated acquisition) for SG-DK (left) and SG (right). In all cases 3× slice and 2× in-plane accelerations were employed with FOV/2 CAIPI shift. The total g-factor calculation times and root-mean-square-errors (RMSE) are reported in the top panels. High level of agreement between the Monte Carlo and analytical g-factor calculation for SG-DK are observed, along with improved g-factor performance for SG-DK as well as improved reconstruction.

Figure 3. Reconstructed images of the acquired 3×3 accelerated dataset (FOV/2 CAIPI shift) using SG-DK (left) and SG (right) reconstructions. Also, shown are the 1/g-factor maps for the SG-DK reconstruction obtained using the Monte Carlo method and the proposed analytical approach. Analytical 1/g-factor map for SG reconstruction is also shown. Good correspondence of the g-factor maps from the Monte Carlo and the analytical approach is observed, with SG-DK again providing markedly improve reconstruction and g-factor performance.

Figure 4. Comparing analytical 1/g-factor maps of the simulated SG-DK reconstruction at different accelerations (MB × Rinplane = 3×1 and 3×3) and blipped-CAIPI shifting (FOV/2, FOV/3 and FOV/4).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
5159