5157
Iterative SENSE with Integrated EPI Nyquist Ghost and Distortion Corrections1Department of Biomedical Magnetic Resonance, Otto-von-Guericke University Magdeburg, Magdeburg, Germany, 2Department of Radiological Technology, Chiang Mai University, Chaigmai, Thailand
Synopsis
The quality of EPI image is intrinsically hindered by Nyquist ghost and geometric distortion which are commonly handled by a 1D non-phase encoded reference and a field map based corrections, respectively. In some cases, a 2D phase reference is required, but scan time is increased. The geometric-mismatch between EPI and coil sensitivities is another concern. Here, the 2D phase correction (without prolonging scan time) and the distortion correction are integrated into a single forward operator rather than considering them consecutively. The results show that the stable reduction in Nyquist ghosting and distortion can improve the tSNR of EPI time series.
PURPOSE:
To improve the accuracy of SENSE-based EPI reconstruction without acquiring the phase reference. The even-odd phase errors and geometric distortions are integrated into a single forward operator rather than considering them consecutively.BACKGROUND:
EPI image quality is intrinsically hindered by two major artifacts, i.e., Nyquist ghost and geometric distortions. To mitigate these artifacts, a 1D non-phase encoded reference1 and a field map based2 techniques are widely used and applied before and after combining the multi-coil images, respectively. In some cases3, a 2D phase correction is required to correct Nyquist ghosting, but an additional full k-space reference scan is needed to measure the 2D phase information. In addition, the geometry mismatch between EPI and coil sensitivity maps4 may not be addressed in post processing.METHODS:
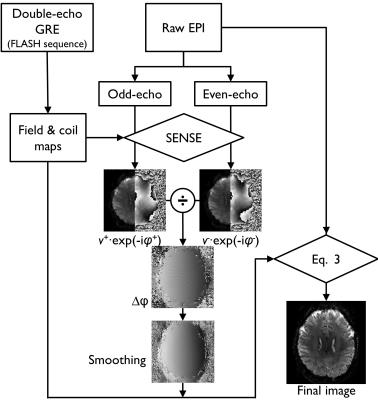
Measurement model and Reconstruction: The discrete EPI samples $$$s$$$ at coil element $$$j$$$ can be written in matrix-vector form [Eq.1]:
$${s^j=\sum_{k=k1}^{k2} M^kEC^j∅^kv+ε, k_1 corresponds\ to\ even\ echo,k_2\ to\ odd\ echo ---1}$$
where $$$v$$$ is the underlying image that we wish to estimate from the noisy data $$$s$$$. $$${E={e}^{-i(Λ[k_x ]r_x+k_yψ[r_y])}}$$$ is denoting the forward encoding operator that accounts for k-space non-uniformity due to the ramp sampling in the readout direction and image distortion caused by B0 inhomogeneity in the phase encoding direction. $$$M$$$ is the binary sampling mask (1=sampled, 0=otherwise). $$$C$$$ is the coil sensitivity. The noise ($$${ε}$$$) is considered white Gaussian. $$${{∅}^{k}}$$$ consists of a set of phases $$$\left\{{e}^{i0} for\ k_1,\ and\ {e}^{i∆φ} for\ k_2\right\}$$$. Note that the phase difference ($$${\left(∆φ=angle(v^{+*} ∙v^{-})\right)}$$$) is estimated using the individual even $$$v^{+}$$$ and odd $$$v^{-}$$$ images which are obtained by iterative SENSE with integrated geometric distortion correction. The * denotes the complex conjugate. The matrix $$$E$$$ represents the discrete Fourier transform (DFT). In practice, the direct computation of $$$E$$$ is computationally intensive. Instead, the NUFFT-based operators5 are used [Eq.2]:
$${E\approx(G_Λ F_Λ D_Λ)iF\left(D_ψ F_ψ G_ψ\right) ---2}$$
where $$$G_Λ$$$ is an oversampled interpolation that maps the undistorted image from a regular grid onto the finer distorted grid $$${ψ[r_y]}$$$. $$${F_ψ}$$$ is an oversampled FFT. $$${D_ψ}$$$ indicates a deapodization operator that accounts for the blurring introduced by $$${G_ψ}$$$. In this work, the distorted grid was computed from the B0 field map2. The inverse FFT $$$iF$$$ transforms the k-space back to image domain. $$$G_Λ$$$ denotes a gridding operator that maps oversampled k-space data from a uniform grid onto the actual k-space trajectory $$$Λ[k_x ]$$$. Finally, the image $$$v$$$ is reconstructed by minimizing the cost function [Eq.3]:
$${\Im(v)=‖s-A(v)‖_2^2+λ‖Lv‖_2^2, with\ A=\sum_{k=k1}^{k2}\sum_{j=1}^{N_c}M^kEC^j∅^k ---3}$$
The Tikhonov regularization with the tri-diagonal regularization matrix ($$$L$$$) is used. The regularization parameter ($$$λ$$$) is a positive integer. Figure 1 is a diagram of the proposed reconstruction.
Data acquisition: Seven healthy volunteers underwent scanning on a whole body 7T (Siemens, Erlangen, Germany) equipped with a 32-channel head coil. All EPI scans with 50 time points were performed using the vendor provided EPI sequence. Double-echo GRE reference data were collected using the FLASH sequence and served to estimate the B0 field maps and coil sensitivity profiles. The conventional (offline) reconstruction comprises 1D phase correction, 1D gridding, coil combination (root-sum-square for R=1, SENSE for R>1), and distortion correction2. The coil sensitivities were estimated using Chatnuntawech’s method6.
RESULTS:
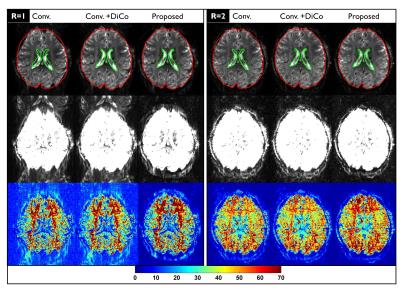
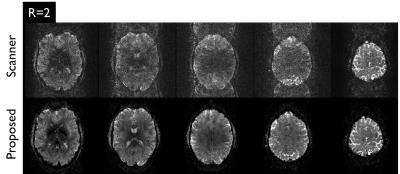
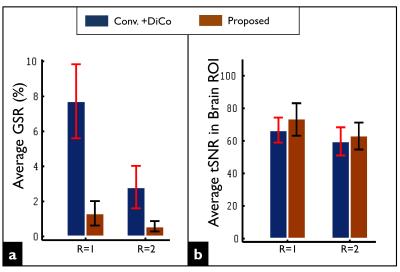
In Figure 2, strong geometric distortions are clearly visible in the fully-sampled image (R=1) obtained by the conventional reconstruction (Conv.). Although such artifacts were largely corrected in the post-processing step (Conv.+DiCo), the intensities of the ghost artifacts were identically high. Although parallel imaging (R=2) remarkably reduced both geometric distortions and Nyquist ghosting, the residual artifacts remained substantially higher compared to the proposed reconstruction. The proposed reconstruction provided higher tSNR values in both R=1 and R=2 data sets. Figure 3 shows noisy images obtained by the vendor’s reconstruction in a case where the phase correction failed. Figure 4 shows the ghost-signal-ratio (GSR) and temporal signal-to-noise-ratio (tSNR) from 7 subjects.DISCUSSION:
We have demonstrated that more accurate EPI images can be achieved when considering the physical effects in a forward signal model, and using the appropriate inverse operators to solve for the uncorrupted image from the redundant data samples from a multi-channel receive array. The stable reduction in Nyquist ghosting and distortion can improve the tSNR of EPI time series. However, the image quality relies on the accuracy of the prior information. For instance, the g-factor related noise will propagate into the final reconstructed image, if the a noisy raw -map is used. In addition, an appropriate coil sensitivity estimation6-8 is required to preserve the phase information. Finally, the proposed reconstruction may be limited when motion occurs between the pre-scan calibration and EPI acquisitions.Acknowledgements
This study was supported by the German Research Foundation DFG (SP632-4) and the National Institutes of Health (1R01-DA021146).References
1) Heid O. Method for phase correction of nuclear magnetic resonance signals. US Patent 5581184; December 03, 1996.
2) Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med 1995; 34(1): 65-73.
3) Xiang QS, Ye FQ. Correction for geometric distortion and N/2 ghosting in EPI by phase labeling for additional coordinate encoding (PLACE). Magn Reson Med 2007; 57(4): 731-741.
4) Griswold MA, Breuer F, Blaimer M, et al. Autocalibrated coil sensitivity estimation for parallel imaging. NMR Biomed 2006; 19(3): 316-324.
5) Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Transactions on Signal Processing 2003; 51(2): 560-574.
6) Chatnuntawech I, McDaniel P, Cauley SF, et al. Single-step quantitative susceptibility mapping with variational penalties. NMR in biomedicine 2016. doi: 10.1002/nbm.3570.
7) Bydder M, Larkman DJ, Hajnal JV. Combination of signals from array coils using image-based estimation of coil sensitivity profiles. Magn Reson Med 2002; 47(3): 539-548.
8) Uecker M, Lai P, Murphy MJ, et al. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014; 71(3): 990-1001.
Figures