5156
Parallel Imaging Reconstruction from Randomly Undersampled Data with k-space Variant Sparsity Constraints1Cardiac Diagnostic Imaging, St. Francis Hospital, Roslyn, NY, United States, 2Radiology, Cincinnati Children's Hospital Medical Center, Cincinnati, OH, United States
Synopsis
A new parallel imaging reconstruction framework is proposed to accelerate MRI using both coil sensitivity and data sparsity. This framework uses random undersampling and performs parallel imaging reconstruction with a k-space variant constraint. No calibration data are needed. It is demonstrated that this new approach offers a gain over conventional parallel imaging in imaging acceleration.
Purpose
The presented work aims to develop a new parallel imaging reconstruction framework that can effectively use both coil sensitivity encoding and data sparsity information. This framework is based on a correlation imaging model1,2 that converts image reconstruction into the estimate of correlation functions. Data acquisition is accelerated by random undersampling. Correlation functions are estimated directly from undersampled data with k-space variant sparsity constraints. Missing samples are estimated with parallel imaging reconstruction in k-space. This approach removes the need for calibration data in conventional parallel imaging. In addition, data sparsity can be utilized to further accelerate imaging.Methods
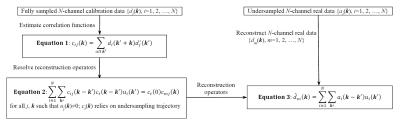
Figure 1 illustrates the correlation imaging model1,2, which provides a mathematical description for parallel imaging. This model may lead to different approaches based on how correlation functions are estimated. For example, if correlation functions are calibrated directly from auto-calibration signals (ACS), the reconstruction is equivalent to GRAPPA. The presented work introduces a new approach to estimating correlation functions from randomly undersampled data with k-space variant constraints. The whole k-space is reconstructed in a region-by-region fashion. Each regional reconstruction follows the steps detailed below:
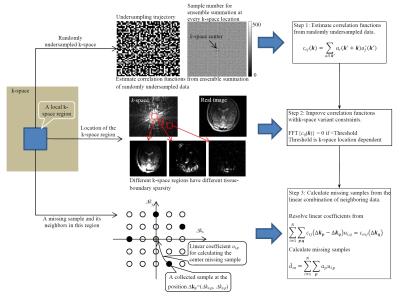
1). Estimate correlation functions from randomly undersampled data: Correlation function is a statistical parameter that may be estimated from a subset of k-space data samples. Ideally, the ensemble summation for every k in Figure 1 (Equation 1) should use the same number of data samples, which is not the case with uniform undersampling. With random undersampling, as shown in Figure 2 (top), the ensemble summation at every k≠0 for a local region uses almost the same number of samples, providing an approach to estimating correlation functions without fully-sampled calibration data.
2). Improve correlation functions with k-space variant sparsity constraints: MRI relies on gradient encoding that decomposes an image into different signal components in a spatial-frequency domain (k-space). The high-frequency components (outer k-space data) arise mostly from tissue boundary that is naturally sparse in the human anatomy. For this reason, k-space data have tissue boundary sparsity increasing with the distance to the k-space center (the increase of spatial frequencies). As a result, if correlation functions are estimated from different k-space regions, they have tissue boundary sparsity that increases from the center to the outer k-space. This tissue-boundary sparsity variation in k-space is used as a constraint in the estimate of correlation functions (Figure 2 center).
3). Calculate missing samples from neighboring data with parallel imaging reconstruction: As illustrated in Figure 2 (bottom), every missing sample is calculated from the linear combination of its neighboring collected samples. The linear coefficients for reconstruction can be resolved from the linear equations determined by estimated correlation functions. It should be noted that these linear equations are not dependent on correlation functions at the k-space center (k=0). For this reason, although the estimate of correlation functions at k=0 may be biased due to the use of more samples in ensemble summation (Figure 2 top), the final parallel imaging reconstruction is not affected.
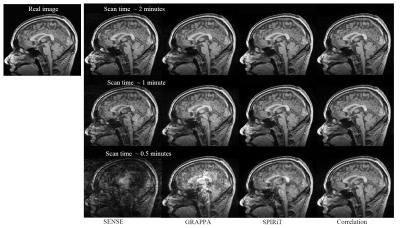
To validate the approach, a set of 3D brain imaging data were collected using a T1-weighted fGRE sequence (FOV 240×240×240 mm, matrix 240×240×154, TR/TE 9.3/4.6 ms, flip angle 8°, ~6 minutes) on a 3T MRI scanner. The coil array for data collection had 8 elements uniformly positioned around the anatomy. The fully-sampled data were manually undersampled to simulate imaging acceleration in the left-right and anterior-posterior directions. SENSE, GRAPPA, and SPIRiT were used as reference approaches.
Results
Figure 2 shows the reconstruction results for a sagittal slice with an imaging acceleration factor of ~10 (corresponding to a data acquisition time of ~30 seconds). Compared with SENSE, GRAPPA, and SPIRiT, the new approach gives better image quality and smaller errors. This improvement is observed in all of our image reconstruction experiments.Discussion
The new technique reconstructs every missing k-space data sample based on a correlation imaging model1,2. Random undersampling allows for the direct calibration of correlation functions from undersampled data, making it possible to further accelerate MRI by reducing calibration data. Using correlation functions estimated with k-space variant constraints, image reconstruction can benefit from neighboring data correlation associated with both coil sensitivity encoding and tissue boundary sparsity, providing a gain over conventional parallel imaging that relies only on coil sensitivity encoding.Conclusion
We have developed a new parallel imaging approach to utilizing coil sensitivity encoding and tissue boundary sparsity to accelerate MRI. This approach can provide a gain in imaging acceleration over conventional parallel imaging.Acknowledgements
This work is supported by NIH/NICHD R21HD071540 and NIH R01EB022405.References
1. Li, Y et al., MRM 2012, 68:2005-2017.
2. Li, Y et al., MRM 2015, 74(6): 1574-1586.
Figures