5082
Reduction of ringing artifacts for high resolution 3D RARE imaging at high magnetic field strengths1Medical Physics Group, Institute of Diagnostic and Interventional Radiology, Jena University Hospital - Friedrich Schiller University Jena, Jena, Germany, 2Hans Berger Department for Neurology, Jena University Hospital - Friedrich Schiller University Jena, Jena, Germany, 3Michael Stifel Center for Data-driven and Simulation Science Jena, Friedrich Schiller University Jena, Jena, Germany, 4Abbe School of Photonics, Friedrich Schiller University Jena, Jena, Germany, 5Center of Medical Optics and Photonics, Friedrich Schiller University Jena, Jena, Germany
Synopsis
High resolution 3D-RARE imaging at 9.4T can be very challenging due to increased artifacts caused by strong T2- and Gibbs ringing. In this work, we present the combination of two correction algorithms, local subvoxel-shift unringing and T2-compensation, to reduce effectively both types of artifacts. For this purpose, the local subvoxel-shift algorithm has been extended to the third spatial dimension and evaluated in healthy mice.
Purpose
High resolution 3D-RARE imaging1 at high field strengths can be very challenging. One of the problems is due to the significantly shortened T2- and at the same time increased T1-relaxation times2 at high magnetic fields that not only reduce the number of deployable 180° refocusing echoes in a single echo train, but also increase the minimum feasible TR for obtaining T2-weighted images without unwanted T1-contrast. In addition, a strong step-wise k-space weighting in phase-encoding direction can cause additional T2-ringing artifacts which overlay with the well-known Gibbs ringing and ultimately limit the application of 3D-RARE imaging as image quality is often severely compromised. In this work, we present the extension of a recently proposed local subvoxel-shift unringing algorithm3 to 3D and combine it with a calibration based k-space weighting for simultaneous reduction of T2-ringing4. The performance of the combination of both correction techniques has been evaluated in healthy mice at 9.4T.Material and Methods
A vendor supplied 3D-RARE imaging sequence with 3D-slab selective excitation and linear ordering of the phase encoding was used as the basis. The sequence was modified to include a short calibration scan at the beginning of each measurement with all encoding gradients turned off, thus essentially sampling the central k-space line of the whole 3D-slab over the 180° readout train4. From this calibration data the mean T2-decay was fitted with an exponential function and used to correct k-space steps in phase encoding direction in the measured data. In the third 3D-encoding direction no correction was necessary as the RARE module was only applied in phase encoding direction.
The algorithm introduced by Keller et al.3 uses subvoxel-shifts to sample and re-interpolate the Gibbs ringing pattern at the zero crossings of the oscillating sinc-function. For application to 2D-data a weighting filter function with a saddle-like structure in k-space was introduced which enhances the ringing in the direction in which unringing is performed, ultimately allowing to perform 1D-unringing separately in each direction. To apply the algorithm also to 3D-data the previously presented 2D-k-space weighting filter3 was extended in the third direction:
$$G_x=\frac{1+\cos k_y}{(1 + \cos k_y) + (1 + \cos k_x)} + \frac{1+\cos k_z}{(1 + \cos k_z) + (1 + \cos k_x)}\\G_y=\frac{1+\cos k_x}{(1 + \cos k_y) + (1 + \cos k_x)} + \frac{1+\cos k_z}{(1 + \cos k_z) + (1 + \cos k_y)}\\G_z=\frac{1+\cos k_y}{(1 + \cos k_y) + (1 + \cos k_z)} + \frac{1+\cos k_x}{(1 + \cos k_z) + (1 + \cos k_x)}$$
to reconstruct three modified versions of the original 3D dataset I, in each of which the ringing is enhanced in one of the three spatial dimensions:
$$I_x=FFT^{-1}\{ FFT\{I \} \cdot G_x \}\\I_y=FFT^{-1}\{ FFT\{I \} \cdot G_y \}\\I_z=FFT^{-1}\{ FFT\{I \} \cdot G_z \}$$
After applying the 1D-unringing described by Keller et al. in x, y and z direction the final image is reconstructed by averaging the three unringed versions of the original image $$$I_{Final}=(I_x+I_y+I_z)/3$$$. Healthy mouse brains (male, C57BL/6J, 6 months old) were measured with the modified 3D-RARE imaging sequence with the following parameters: 240x180x160 encoding matrix, 24x18x6mm FOV, 1600ms TR, 5.3ms echo spacing, 150kHz acquisition bandwidth and RARE-factor of 20. The resulting isotropic image resolution was 100µm with TA of 40 minutes and an effective k-zero TE of 53ms. Image reconstruction was performed offline with four different settings: 1) no T2-compensation and no 3D-unringing, 2) no T2-compensation and 3D-unringing, T2-compensation and no 3D-unringing and 4) both T2-compensation and 3D-unringing. All measurements were performed on a 9.4T Bruker BioSpec USR-94/20 MR scanner using a 2-channel quadrature cryoprobe.
Results
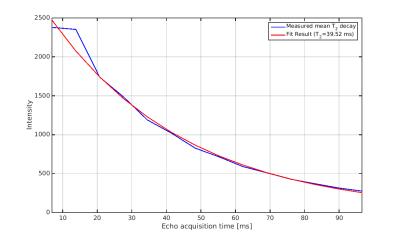
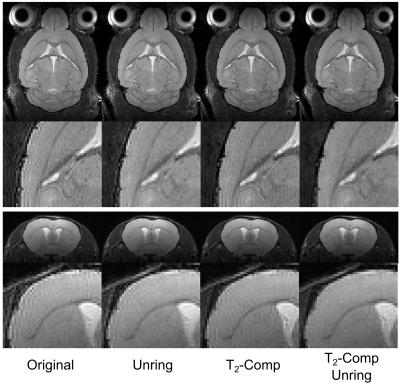
The calibration measurement (Fig. 1) resulted in a mean T2-decay of 39.52ms with good agreement to a mono-exponential function (R2=0.987). Imaging results of the in vivo experiments are shown in Figure 2 for coronal and transverse slice orientation of the mouse brain. Without any correction strong ringing artifacts are visible not only around the border of the brain but also in deeply located brain regions. Applying only 3D-unringing or T2-compensation reduces these artifacts significantly but not completely. With either correction noticeable ringing artifacts still remain. Only with both correction methods applied together - T2-compensation and 3D-unringing - artifacts are further suppressed. In addition to ringing artifacts T2-blurring is also visible on the images, especially in the ventricles, which is distinctly reduced with T2-compensation.Discussion and Conclusion
Combining T2-decay compensation with 3D-unringing, troublesome image artifacts can be significantly reduced in high resolution 3D RARE imaging at high field strengths. Applying only one of the corrections methods was not sufficient to remove the majority of artifacts, suggesting that both sources for these artifacts are present and complementary. The applied methods are both easy to implement since they only require minor modifications of the imaging sequence and can be combined with fast and simple post-processing. Our proposed calibration and correction scheme should be especially of interest when alternative, but more complex optimized three-dimensional fast-spin-echo MRI sequences5, like CUBE, SPACE or VISTA are not available, as is typical the case with pre-clinical high-field small animal imaging MR systems.Acknowledgements
No acknowledgement found.References
1. Hennig J, Nauerth A, Friedburg H. RARE imaging: A fast imaging method for clinical MR. Magn Reson Med. 1986;3:823–833
2. de Graaf RA, Brown PB, McIntyre S, Nixon TW, Behar KL, Rothman DL. High magnetic field water and metabolite proton t1 and t2 relaxation in rat brain in vivo. Magn Reson Med. 2006;56:386–394.
3. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local sub-voxel-shifts. Magn Reson Med. 2016;76:1574–1581.
4. Zhou X, Liang ZP, Cofer GP, Beaulieu CF, Suddarth SA, Johnson GA. Reduction of ringing and blurring artifacts in fast spin-echo imaging. J Magn Reson Imaging. 1993;3:803–807.
5. JP Mugler III. Optimized Three-Dimensional Fast-Spin-Echo MRI. J Magn Reson Imaging. 2015;39:745-767
Figures