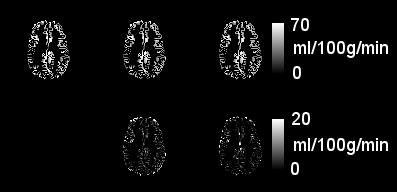Synopsis

Arterial spin labelling (ASL) offers valuable measurements of perfusion in the brain and other organs. However, ASL data have low SNR and are prone to partial volume effects. We present a Bayesian model of anatomically-derived spatial correlation in ASL data (ADRIMO), which improves the accuracy of perfusion estimates and hence improves the analysis of ASL data. The method is assessed experimentally by examining ASL images from a cohort of 130 preterm-born adolescents.

Introduction

Methods

We formulate a probabilistic model, relating ASL images, $$$y$$$, to the underlying perfusion values, $$$f$$$, at each voxel. We assume each region (as defined by the lobar parcellation) contains voxels with normally distributed perfusion values, with mean $$$\mu$$$ and covariance $$$\Sigma_\mu$$$, which are also inferred in the model:

$$p(f, \mu, \Sigma_\mu | y) \propto p(y | f, \mu, \Sigma_\mu) p(f, \mu, \Sigma_\mu) = p(y | f) p(f | \mu, \Sigma_\mu) p(\mu, \Sigma_\mu)$$

$$p(f | \mu, \Sigma_\mu) = \prod_i \mathcal{N}(f_i; \mu,\Sigma_\mu)$$

To find the data likelihood, we integrate the signal model, $$$g(f)$$$, over the Gaussian measurement noise $$$\sigma_n$$$:

$$p(y | f) = \int_{\sigma_n}\prod_j \mathcal{N}(y_j; g(f),\sigma_n)$$

As in a similar method for IVIM⁴ we use a Monte Carlo Markov Chain to jointly infer the per-voxel perfusion and the underlying per-region distribution parameters. Here we use the ASL signal model of Buxton et al⁵, with regions defined by a lobar parcellation of the brain⁶. We use a noninformative Jeffreys prior for $$$p(\mu,\Sigma_\mu)$$$.

For experimental validation, we use imaging data from a cohort of 130 adolescents at 19 years of age. Data for 81 extremely preterm (EP) adolescents (F/M=48/33, mean birth gestation= 24.8±0.8wks) and 49 (F/M=31/18) term-born socioeconomically matched peers were acquired on a 3T Phillips Achieva. We acquired Pseudo-Continuous ASL (PCASL) for 30 control-label pairs with PLD=1800ms+41ms/slice, label duration τ=1650ms (resolution 3x3x5mm) using 2D EPI. We compare the first half of the dataset with the second to perform test-retest experiments, comparing ADRIMO’s repeatability with simple voxelwise fitting and 5mm FWHM smoothing. Subsequently, we use the full dataset to show ADRIMO more reliably detects perfusion differences between groups. We investigate differences by gestational age at birth (GAB), by sex and by method of delivery (caesarean). Finally we explore correlations between haematocrit levels and GM perfusion.

Results and Discussion

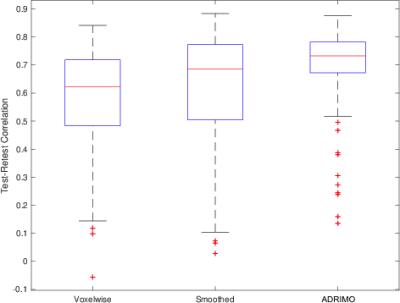
Example perfusion images are shown in Figure 1. Visually, ADRIMO is smoother than voxelwise fitting and less smooth than blurring. This is unsurprising: ADRIMO uses broad spatial correlations on the scale of regions, rather than localised correlations on the scale of voxel neighbourhoods. High smoothness may be undesirable: blurring neighbouring values may drag voxels away from their true values. Test-retest correlations are significantly higher in ADRIMO, compared with standard voxelwise fitting (R=0.69±0.13 vs R=0.57±0.17, P=0.0026) and Gaussian smoothing (R=0.62±0.20, P=0.023), as summarised in Figure 2.

All methods, when used to estimate average GM perfusion, show significant differences between terms and preterms (P=1.8E-4 and d=0.70 with ADRIMO, perfusion T/P 53.6±10.8/46.8±9.0 ml/100g/min, P<0.05 with all). All methods find differences between preterm males and preterm females (P=3.5E-5 and d=0.88 with ADRIMO, perfusion F/M 52.3±10.2/44.9±8.6 ml/100g/min, P<0.01 with all), and no method shows significant differences between term-born males and females (P>0.05). ADRIMO shows these differences with higher statistical power in each case. This could reduce sample sizes, or allow more certain conclusions for a given sample size. Similarly, all three methods show no significant difference between Caesarean/non-Caesarean (P>0.05), where no difference is expected.

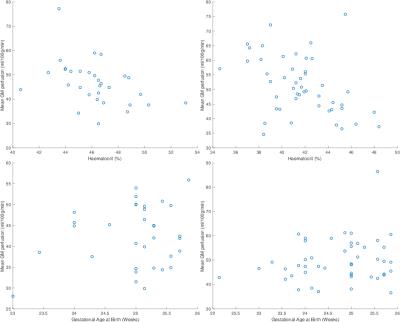
Plots of perfusion against haematocrit and GAB are shown in Figure 4. Testing for rank correlation between perfusion and haematocrit reveals a negative relationship in male and female subjects. This remains after correction for GM volume (R=-0.43, -0.52 respectively, P=0.0058, 0.0042 with ADRIMO and P<0.02 for all methods). Testing for correlation between perfusion and GAB within preterms does not reveal an association, suggesting that despite the perfusion difference between groups, there is little evidence for this increasing with the extent of prematurity — at least within the spread of three gestational weeks covered by this dataset.

Conclusion

Acknowledgements

References

[1] Asllani, I., Ajna B., and Brown, T. R. "Regression algorithm correcting for partial volume effects in arterial spin labeling MRI." Magnetic Resonance in Medicine 60.6 (2008): 1362-1371.

[2] Alsop, D. C., Detre, J. A., Golay, X., Günther, M., Hendrikse, J., Hernandez-Garcia, L., ... & Osch, M. J. (2015). Recommended implementation of arterial spin-labeled perfusion MRI for clinical applications: A consensus of the ISMRM perfusion study group and the European consortium for ASL in dementia. Magnetic resonance in medicine, 73(1), 102-116.

[3] Chappell, M. A., Groves, A. R., MacIntosh, B. J., Donahue, M. J., Jezzard, P., & Woolrich, M. W. (2011). Partial volume correction of multiple inversion time arterial spin labeling MRI data. Magnetic resonance in medicine, 65(4), 1173-1183.

[4] Orton, M. R., Collins, D. J., Koh, D. M., & Leach, M. O. (2014). Improved intravoxel incoherent motion analysis of diffusion weighted imaging by data driven Bayesian modeling. Magnetic resonance in medicine, 71(1), 411-420.

[5] Buxton, R. B., Frank, L. R., Wong, E. C., Siewert, B., Warach, S., & Edelman, R. R. (1998). A general kinetic model for quantitative perfusion imaging with arterial spin labeling. Magnetic resonance in medicine, 40(3), 383-396.

[6] Cardoso, M. J., Modat, M., Wolz, R., Melbourne, A., Cash, D., Rueckert, D., & Ourselin, S. (2015). Geodesic information flows: spatially-variant graphs and their application to segmentation and fusion. IEEE transactions on medical imaging, 34(9), 1976-1988.