Synopsis

This work introduces a new framework for myelin water fraction (MWF) estimation. We use a novel scan design approach to construct a sequence a fast steady-state sequences and optimize corresponding flip angles and repetition times for precise MWF estimation. We quantify MWF and five other parameters per voxel using a novel method based on kernel ridge regression. We obtain MWF maps in vivo that are comparable to those reported in literature, with possibly shorter overall scan time.

Introduction

Myelin loss is central to the pathogenesis of several neurodegenerative diseases. Myelin quantification is therefore of interest for monitoring the development and progression of WM disorders.

Bulk MR signal arises from multiple water compartments with different relaxation rates, and the fastest-relaxing compartment is due to water trapped between myelin bilayers¹. "Myelin water fraction" (MWF) denotes the proportion of signal arising from the fast compartment relative to total signal, and is an indirect measure of myelin content.

Multiple spin-echo (MSE) acquisitions¹ and accelerated variations² yield MWF estimates in agreement with in vitro measurements³ but are limited by long repetition times TR. Existing short-TR steady-state (SS) sequences are faster, but produce MWF estimates^4,5 that disagree with MSE measurements⁶, possibly due to insufficient estimation precision⁷.

This work introduces a new SS acquisition for fast, precise MWF estimation. We design the flip angles and repetition times of combinations of spoiled gradient-recalled echo (SPGR) and dual-echo steady-state (DESS) sequences to optimize MWF estimation precision. We estimate MWF and five other parameters using a novel method based on kernel ridge regression⁸ (KRR). We obtain MWF maps in vivo that are comparable to those reported in MSE literature.

Methods

This section adapts a general method for acquisition design⁹ to formulate a cost function that characterizes MWF estimator variance. The method seeks to minimize this cost through a novel greedy optimization procedure.

After image reconstruction, a sequence of scans (e.g., SPGR and DESS) useful for MWF estimation produce at each voxel position a sequence of noisy voxel values $$$\mathbf{y} \in \mathbb{C}^D$$$, modeled as

$$\mathbf{y}=\mathbf{s}(\mathbf{x};\kappa,\alpha,\mathbf{T}_\mathrm{R})+\mathbf{n},$$

where $$$\mathbf{x}\in\mathbb{R}^L$$$ denotes $$$L$$$ latent parameters; $$$\kappa\in\mathbb{R}$$$ denotes (separately acquired and estimated) flip angle variation; $$$\alpha,\mathbf{T}_\mathrm{R}\in\mathbb{R}^D$$$ denote prescribed flip angles and repetition times; $$$\mathbf{s}:\mathbb{R}^L\times\mathbb{R}\mapsto\mathbb{C}^D$$$ models the noiseless signals arising from $$$D$$$ datasets; and $$$\mathbf{n}\in\mathbb{C}^D$$$ is complex zero-mean Gaussian noise with covariance $$$\Sigma$$$. We take $$$\mathbf{s}$$$ to model two non-exchanging water compartments. Neglecting across-compartment variation in off-resonance effects, this reduces model dependencies to six free latent parameters per voxel: MWF $$$f_\mathrm{M}$$$; (spin-lattice, spin-spin) relaxation time constants for the myelin water $$$(T_1^\mathrm{M},T_2^\mathrm{M})$$$ and slow-relaxing $$$(T_1^\mathrm{S},T_2^\mathrm{S})$$$ compartments; and proportionality constant $$$m_0$$$. We collect these $$$L\gets6$$$ unknowns as $$$\mathbf{x}\gets[f_\mathrm{M},T_1^\mathrm{M},T_2^\mathrm{M},T_1^\mathrm{S},T_2^\mathrm{S},m_0]^\mathsf{T}$$$.

The Cramer-Rao Bound (CRB) states that the covariance of any unbiased estimator of $$$\mathbf{x}$$$ is bounded below by the inverse of the Fisher information matrix

$$\mathbf{F}(\mathbf{x};\kappa,\alpha,\mathbf{T}_\mathrm{R}):=[\nabla_\mathbf{x}\mathbf{s}(\mathbf{x};\kappa,\alpha,\mathbf{T}_\mathrm{R})]^\mathsf{H}\Sigma^{-1}[\nabla_\mathbf{x}\mathbf{s}(\mathbf{x};\kappa,\alpha,\mathbf{T}_\mathrm{R})].$$

For precise MWF estimation, we seek $$$\alpha,\mathbf{T}_\mathrm{R}$$$ that achieve small (unbiased) MWF estimator variance lower bound $$$[\mathbf{F}^{-1}(\mathbf{x};\kappa,\alpha,\mathbf{T}_\mathrm{R})]_{(1,1)}$$$ for a range of typical $$$\mathbf{x},\kappa$$$ values. We seek to (locally) minimize the objective function

$$\Psi(\alpha,\mathbf{T}_\mathrm{R}):=\mathbb{E}_{\mathbf{x},\kappa}([\mathbf{F}^{-1}(\mathbf{x};\kappa,\alpha,\mathbf{T}_\mathrm{R})]_{(1,1)}),$$

where $$$\mathbb{E}_{\mathbf{x},\kappa}$$$ denotes expectation with respect to assumed and measured distributions of $$$\mathbf{x}$$$ and $$$\kappa$$$, respectively.

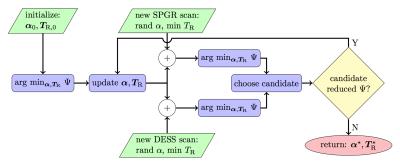
Since $$$\Psi$$$ is nonconvex in $$$\alpha,\mathbf{T}_\mathrm{R}$$$, local optimizers depend on initialization. Moreover, it is unclear a priori how to best allocate scan time amongst initial SPGR/DESS scans, under a given total time constraint. Figure 1 diagrams our approach that greedily constructs a scan combination through a sequence of constrained optimization problems interleaved with SPGR/DESS scan additions. Table 1 lists optimized scan parameters found by our greedy design.

In all experiments, we estimated six parameters per voxel from SPGR/DESS data via non-iterative KRR⁸ initialization, followed by iterative local optimization. We evaluate only MWF estimates in the following.

Experimentation and Results

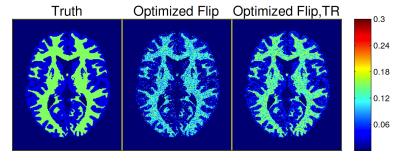
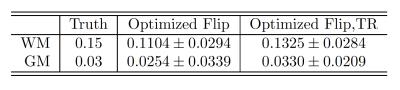
We first show through BrainWeb¹⁰ simulations how greedy scan construction can find desirable scan combinations. Figure 2 and Table 2 demonstrate that for a given total scan time, the proposed acquisition (Table 1) consisting of 4 SPGR and 3 DESS scans with optimized flip angles and repetition times outperforms a sequence of 9 SPGR and 9 DESS scans with fixed minimum TR.

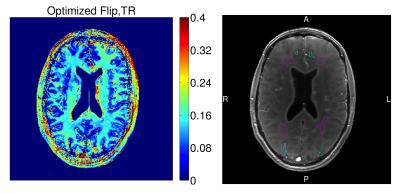
We next estimate MWF in vivo using the proposed acquisition. We collected 3D axial SPGR/DESS data from a 32-channel Nova receive head array in a 3T GE scanner using optimized flip angles and repetition times and fixed 4.67ms echo time; $$$256\times256\times8$$$ matrix size; and $$$24\times24\times4$$$cm³ field of view. We also collected two Bloch-Siegert (BS) SPGR scans for separate $$$\kappa$$$ estimation¹¹. SPGR/DESS and BS acquisitions respectively took totals of 10m8s and 1m40s.

Figure 3 provides representative MWF estimates and compares corresponding sample statistics with WM/GM regions of interest (ROIs). MWF sample means in WM are comparable to those in recent MSE studies².

Summary

Acknowledgements

References

1. MacKay A, Whittall K, Adler J, Li D, Paty D, and Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Mag. Res. Med. 1994;31(6):673-677.

2. Prasloski T, Rauscher A, MacKay A, Hodgson M, Vavasour I, Laule C, and Madler B. Rapid whole cerebrum myelin water imaging using a 3D GRASE sequence. Neuroimage. 2012;63(1):533-539.

3. Morell P. Myelin. Springer. 1984.

4. Deoni S, Rutt B, Arun T, Pierpaoli C, and Jones D. Gleaning multicomponent T1 and T2 information from steady-state imaging data. Mag. Res. Med. 2008;60(6):1372-1387.

5. Deoni S. Correction of main and transmit magnetic field (B0 and B1) inhomogeneity effects in multicomponent-driven equilibrium single-pulse observation of T1 and T2. Mag. Res. Med. 2011;65(4):1021-1035.

6. Zhang J, Kolind S, Laule C, and MacKay A. Comparison of myelin water fraction from multiecho T2 decay curve and steady-state methods. Mag. Res. Med. 2015;73(1):223-232.

7. Lankford C and Does M. On the inherent precision of mcDESPOT. Meg. Res. Med. 2013;69(1):127-136.

8. Nataraj G, Nielsen J, and Fessler J. Dictionary-free MRI parameter estimation via kernel ridge regression. Proc. IEEE Intl. Symp. Biomed. Imag. 2017, submitted.

9. Nataraj G, Nielsen J, and Fessler J. Optimizing MR scan design for model-based T1, T2 estimation from steady-state sequences. IEEE Trans. Med. Imag. 2016, to appear.

10. Collins D, Zijdenbos A, Kollokian V, Sled J, Kabani N, Holmes C, and Evans A. Design and construction of a realistic digital brain phantom. IEEE Trans. Med. Imag. 1998;17(3):463-468.

11. Sacolick L, Wiesinger F, Hancu I, and Vogel M. B1 mapping by Bloch-Siegert shift. Mag. Res. Med. 2010;63(5):1315-1322.