Synopsis

At high field strengths, cardiac cine acquisitions acquired with balanced SSFP can suffer from banding artifacts. To mitigate this issue, dynamically phase-cycled cardiac cine was acquired in a single breathhold with undersampling rates of 4 and 6, and images were reconstructed with a phase-cycle banding profile regularization that exploits redundancy between phase-cycles.

Purpose

Methods

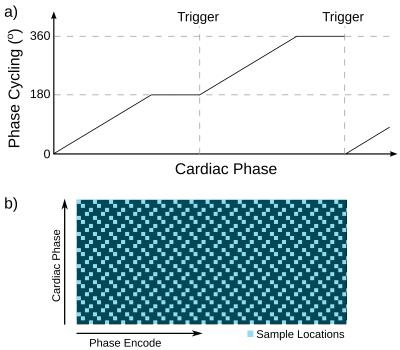
The dynamic phase cycling scheme is depicted in Fig. 1a [1]. The phase cycle was incremented through 180 degrees over 23 cardiac phases every heartbeat, then kept constant until the next trigger. The net result is two effective phase-cycles (differing by 180° with respect to each other) acquired in interleaved heartbeats.

Reconstructions were performed by solving:$$(1)\quad\underset{x}{\arg\min}\left\|SFC_Rx-k_s\right\|_2^2+\mu_p\left\|Rx\right\|_1+\mu_w\left\|\Psi x\right\|_1$$where $$$x$$$ is the image, $$$C_R$$$ represents receiver sensitivity profiles, $$$F$$$ is a two-dimensional FFT, $$$S$$$ is k-space sampling, $$$k_s$$$ is the acquired data, $$$R$$$ is a transform that exploits redundancy between phase-cycling banding profiles (defined below), $$$\Psi$$$ is a 3-dimensional wavelet transform over two spatial dimensions and time [2], and $$$\mu_p$$$ and $$$\mu_w$$$ are parameters that control the regularization strength.

$$$R$$$ is defined under the assumption that bSSFP banding can be approximated by multiplication of the “true” image by a banding-profile (i.e., analogous to receiver sensitivities). That is, $$$x_i=P_ix$$$, where $$$P_i$$$ is the banding profile for the $$$i$$$’th phase-cycle. Thus for two phase-cycles, as is the case here, $$$P_1x_2-P_2x_1=0$$$, and at every voxel location, $$$v$$$, $$$R_v=[-P_{2,v},P_{1,v}]$$$.

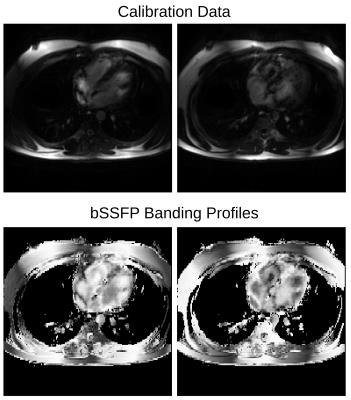
Uniform undersampling was used for each frame, with acquired samples shifted every cardiac phase (Fig. 1b). Receiver sensitivity profiles were estimated using ESPIRiT [3] using calibration data generated by averaging over all time. The banding profiles slowly vary over time due to dynamic phase-cycling; therefore, calibration data for their estimation, $$$M$$$, was generated by a sliding window time-average of the undersampled k-space data. The banding profiles were then estimated using:$$(2)\quad P_i=\frac{M_i}{\sum_iM_i}$$The final banding-profiles used in $$$R$$$ were obtained by normalizing the result of Equation 2 by its root-square-sum over phase-cycles, which mitigates noise amplification resulting from division in Equation 2 (e.g., Fig. 2).

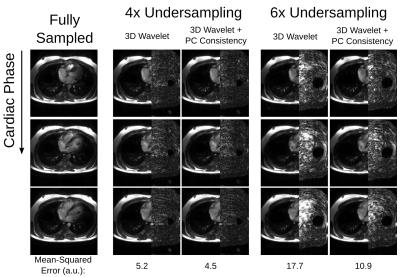
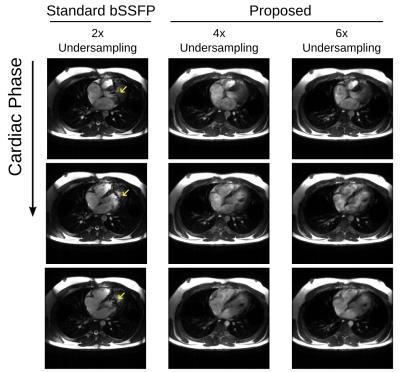
To demonstrate the method, data was acquired in a volunteer on a 1.5 T GE Signa Excite with 8 receiver channels. The bSSFP parameters common to all scans were a 3.4 ms TR, 1.4 ms TE, 24x24 cm2 FOV, 8 mm slice thickness, and 10 views per segment (34 ms temporal resolution). A fully sampled axial scan was acquired with resolution 1.25x1.85 mm² in a breath-hold of 27 heartbeats, and was retrospectively undersampled by both R = 4 and R = 6. Prospectively undersampled axial scans with resolution 1.25x1.5 mm² were also acquired in 9 heartbeats with R = 4 and 7 heartbeats with R = 6. A typical bSSFP scan with only one phase-cycle of 180 degrees and rate 2 undersampling was also acquired in 9 heartbeats. In all cases, the gradient shim was deliberately offset from optimal to create increased off-resonance along the left-right direction. Two different reconstructions were performed with the following regularization schemes: (1) 3D wavelet only; (2) 3D wavelet and phase-cycle redundancy (i.e., Equation 1). Optimal $$$\mu$$$ were determined separately for each of the two reconstructions by minimizing the mean-squared-error of images reconstructed from the retrospectively undersampled data.

Results and Discussion

For the retrospectively undersampled data, the proposed method results in the lowest error (Fig. 3). The standard bSSFP scan exhibits severe banding artifacts, but the proposed method with prospective undersampling generates band-free images with similar scan time (Fig. 4).

It is also possible to directly enforce banding profiles in the data consistency term of the objective function rather than the separate regularization term used here. However, blood flow causes disturbances in the bSSFP steady-state, which reduce the accuracy of the banding estimates. Using regularization allows tailoring of how strictly the banding profiles are enforced, ultimately resulting in more accurate reconstructions. In addition, it would be relatively straightforward to extend this method to use pseudo-random undersampling schemes similar to VISTA [2], which would likely improve the benefits of wavelet regularization and render view-sharing errors in banding-profile estimation more benign.

Acknowledgements

References

1. Datta A, Baron CA, Ingle RR, Cheng JY, Nishimura DG. Breath-held phase-cycled cardiac CINE MRI using slow frequency modulation. Proceedings of the 24th Annual Meeting of ISMRM, Singapore, 2016. p. 3214

2. Ahmad R, Xue H, Giri S, Ding Y, Craft J, Simonetti OP. Variable density incoherent spatiotemporal acquisition (VISTA) for highly accelerated cardiac MRI. MRM 2015;74(5):1266-78

3. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. MRM 2014;71(3):990-1001