Introduction

MRI with non-linear spatial encoding magnetic fields (SEM) can provide high quality MR images, but there images are usually calculated using iterative optimization procedures. Such reconstruction methods can take a long time to converge, and the results may depend on the initial iteration parameters. We propose a fast, non-iterative image reconstruction method for O-space imaging¹ based on the local K-space and local SEMs². Preliminary results based on an analytical phantom are presented.

Theory

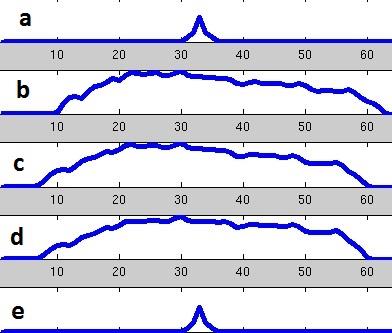
In general, O-space imaging with arbitrary k-space trajectories can be expressed as $$s(t)=\int_{(x,y)\in{I}}^{} m(x,y)e^{j2\pi\gamma\mu(x,y,t)}dxdy=\int_{(x,y)\in{I}}^{} m(x,y)e^{j2\pi[xk_x+yk_y+\gamma(x^2+y^2)G_Ot]}dxdy \space\space (1)$$ When the readouts are radial projections: $$s(t)=\int_{(r,\theta)\in{I}}^{} m(r,\theta)e^{j2\pi\gamma[rG_{xy}+r^2G_O]t}rdrd\theta \space\space (2) $$ in which the phase is only relevant to r. Since the non-linear SEM is radial, we have encoding frequency: $$\omega(r)=\gamma\frac{\partial \mu}{\partial t}=\gamma(rG_{xy}+r^2G_O) \space\space (3)$$ Its linear approximation $$\omega(r)\approx\omega(r_0)+\frac{\partial \omega}{\partial r_0}(r-r_0)=\gamma(r_0G_{xy}+r_0^2G_O)+\gamma(G_{xy}+2r_0G_O)(r-r_0) \space\space (4)$$ at r₀ with the local k-space $$K(r_0), k_r|_{r=r_0}=\gamma\frac{\partial \mu}{\partial r}|_{r=r_0}$$ For simplicity, we choose the local K-space located at r₀=0, Eq 2 becomes $$s(t)=\int_{(r_L,\theta)\in{I}}^{} m(r_L,\theta)e^{j2\pi\gamma r_LG_{xy}t}r_Ldr_Ld\theta \space\space (5)$$ for which IFT methods could be used for image reconstruction after the position and intensity corrections described below. Non-linear correction: 1D FFT in the radial direction will give r_L so we can the solve the following equation for r that will be used for resetting the position: $$rG_{xy}+r^2G_O=r_LG_{xy}$$ The derivative of (3), $$\frac{\partial \omega(r)}{\partial r}=\gamma(G_{xy}+2rG_O)$$ which dictates the local stretch in r, will be used for intensity correction. The corrected 1D signal is then IFFT'd back to raw K-space and 2D IFT can be used for 2D image reconstruction.

Results

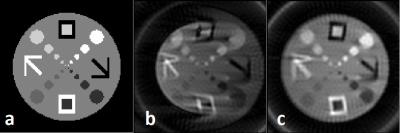
An analytical phantom (Fig 2a) was used to generate the k-space data according to Eq 2 with the following parameters: Gxy=18.35mT/m, Go=0.025mT/m, 64 projections covering the 2D and 64 readouts per projection but the O-center only sweeps the left 180^o. The 1D position and intensity correction in one projection are illustrated in Fig 2. The k-space data were first corrected used the proposed method, then after correction the conjugate phase method³ was employed to reconstruct the images (Fig 2c). For comparison, if the same conjugate phase method was applied directly on the raw data without any correction, reconstruction results are shown in Fig 2b.

Discussion and Conclusions

This work introduces and demonstrates the effectiveness of a fast, non-iterative method for image reconstruction of nonlinear O-space imaging data. Residual distortions and intensity non-uniformities in the image near the edges still exist, as shown in Fig 2c. This might be due to the approximation of Eq 2 with a linear form of Eq 5, by a single local k-space located at r₀=0. Further investigation is needed to refine the distortion and intensity correction. This approach can also incorporate multiple local k-space data set with a multi-channel RF parallel acquisitions, for further reductions in image distortion. Also needed is a more elaborate implementation of the conjugate phase method for a better evaluation of the reconstruction efficacy.

Acknowledgements

This work is supported by the NIH under grant NIH R01 EB076978.