Introduction

MR Fingerprinting (MRF)^1,2 has been introduced as a new technique for quantitative MRI. It can be used for MR parameter encoding (T1, T2, etc.). A compromise between the parameter encoding and the spatial encoding dimension is made to reduce the total scanning time. Therefore, efficient spiral sampling was proposed in combination with under-sampling¹. After gridding the measured spiral k-space data, dictionary matching is performed to identify tissue properties¹. However, although the spiral is very efficient in terms of sampling, it is sensitive to all kinds of off-resonance effects resulting in signal blurring³. This effect leads to geometric distortion as well as to degraded MRF parameter estimation accuracy. To overcome these limitations, the present work proposes to combine spiral-based MRF with appropriate field-map-based deblurring (e.g. via ^3,4). The basic feasibility of this approach with and without under-sampling is shown in phantom and in-vivo experiments.

Methods

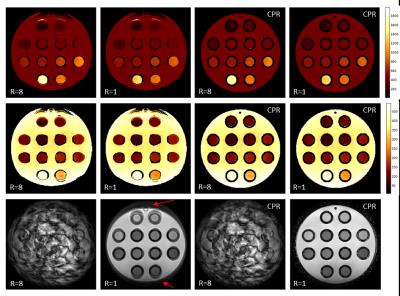
Using a B0 field map and a conjugate phase reconstruction (CPR)⁴, off-resonance effects in conventional spiral imaging can be removed during reconstruction or as a post-processing step. However, in case of k-space under-sampling, where the Nyquist criterion is not fulfilled, the application of CPR is problematic. In an under-sampled spiral image, each voxel is contaminated by fold-over from other spatial locations⁵, spoiling the unique spatial relationship between voxel signal and off-resonance, meaning that the deblurring result is by far not correct. However, rotating the spiral under-sampling pattern in MRF from shot to shot results in the folding signal part for each CPR-corrected voxel to change incoherently in time, whereas the true voxel signal does not. Accordingly, applying a voxel-specific demodulation works correctly for the true signal part. It does not change the properties of the under-sampling aliasing, which is then suppressed by the MRF matching process, making CPR for MRF work. This approach was implemented and tested in a phantom (Diagnostic Sonar, Eurospin II) and in vivo (five healthy volunteers) on a 3T MR system (Philips, Achieva) with an eight-channel head coil. The spoiled gradient-echo MRF sequence² had 250 RF shots: a flip angle ramp from 0° to 60° over 120 steps, followed by a constant part with 60° over 130 steps. This sequence was preceded by spin inversion (inversion time 20ms). TR was fixed to 30ms, TE was fixed to 3ms. A variable frequency spiral readout (AQ-window: 20ms, 16 interleaves) was used to acquire a 2D slice (FOV/pixel size: 230/1.0mm²) with 8mm slice thickness. The total scan time without under-sampling was 2:16min. Different under-sampling factors R=2, 4, 8, 16 were used. A corresponding B0 field map was obtained using a Cartesian dual-acquisition gradient echo scan, matching the resolution of a fully sampled spiral using TE/TR: 5/10ms employing a TE increment of 2.3ms (W/F in-phase) with 2.6s total scanning time. Gridding reconstruction, complex coil combination, and subsequent CPR were performed for each MRF encoding step followed by dictionary-based voxel-wise signal evaluation².

Results

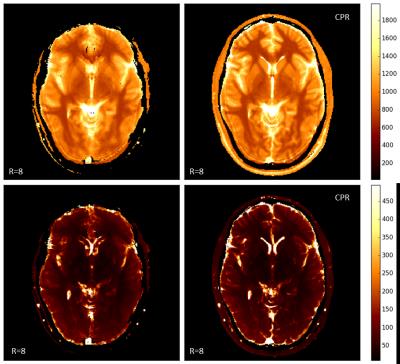
Figure 1 shows selected results from the phantom scans. All maps derived from the uncorrected reconstructions show strong geometric distortions and incorrect matching at the position of the two uppermost tubes. CPR reconstruction from the same measured data removes the distortions, independent of the under-sampling factor. For the fully sampled scans, the distortions are also visible in the underlying image data. Figure 2 shows T1 and T2 maps from one of the volunteers (under-sampling factor R=8, scan time 17s). The uncorrected maps show strong blurring at the position of the ventricle and geometric distortion at the frontal lobe, which is not visible in the CPR reconstructions.

Discussion

Although CPR is theoretically not applicable to under-sampled data, it works in combination with MRF and shows significant improvements in image quality. It can allow for a more effective spiral sampling in MRF by choosing a longer acquisition window. Here the field map was obtained from a separate scan, but it is conceivable to estimate the field map from the acquired MRF data themselves¹. This can be done by first using MRF to estimate B0 from the under-sampled, uncorrected data, followed by an off-resonance compensated MRF reconstruction. For the time being the use of CPR, although it is only a simple approximation, is a feasible approach to improve geometric and parameter estimation accuracy in MRF. In the future, off-resonance correction will have to be integrated in more sophisticated MRF reconstruction approaches.

Acknowledgements

No acknowledgement found.