5065
Non-rigid Groupwise Registration for Intravoxel Incoherent Motion Imaging of the Heart1Institute for Biomedical Engineering, ETH Zurich, Zurich, Switzerland
Synopsis
Intravoxel Incoherent Motion (IVIM) imaging is an attractive approach for contrast-agent free in vivo perfusion measurement in the heart. Since the data is acquired during free breathing, nonrigid respiratory motion is considerable and needs to be corrected before estimation of IVIM parameters. In order to provide accurate image registration, an approach with parametric total variation regularization of displacements and low-rank structure of aligned images stack is presented. The proposed method allows for robust IVIM parameter estimation and improves mean squared residuals of the IVIM model by 24% on average compared to state-of-the-art non-rigid registration methods.
Introduction
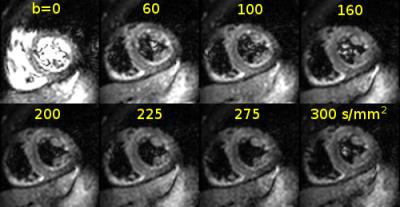
Intravoxel Incoherent Motion (IVIM) imaging of the in vivo heart [1] is an active research topic [2,3] as the method potentially allows mapping of perfusion related parameters in the myocardium without requiring contrast agent injection. However, respiratory motion during in vivo imaging requires methods for image registration. The presence of breathing motion leads to non-rigid displacement fields with discontinuities at sliding interfaces. Such motion cannot be accurately represented with generic smoothness regularization. In this work we present a 2D cardiac IVIM registration method based on a parametric total variation regularization[4]. To leverage long imaging sequences, we perform groupwise registration by adopting a principal component analysis (PCA)-based image similarity metric [5]. The PCA (or nuclear) metric accounts for nonuniform image irregularities, such as a bright blood pool and contrast variation at different b-values (Figure 1).Methods
Data acquisition
A second-order motion compensated diffusion-weighted spin-echo EPI sequence [6] was used on a 1.5T Philips Achieva system (Philips Healthcare, Best, The Netherlands) equipped with a 32-channel cardiac receiver coil array. Short-axis diffusion images at a mid-ventricular level were acquired with following parameters: spatial resolution of 2.4×2.4 mm2, slice thickness of 10 mm, 15 b-values, 6 diffusion directions (for b>0 s/mm2) and 4 averages. The data acquisition was conducted during free-breathing of the subjects (Figure 1).
Image registration
We represent each of $$$N$$$ 2D images as a real vector $$$f_i$$$ of length $$$L$$$, where $$$L$$$ is the number of pixels in the image. Each image is accompanied by a displacement field $$$d(t_i)$$$, that is parametrized by 1st order B-splines [4] with coefficients $$$t_i$$$. Image warping is denoted as $$$f_i\circ d(t_i)$$$. Since aligned images share positions of prominent structures, we assume that residual intensity variation has a low dimensionality [5]. Such a constraint is implemented by using the nuclear norm of the stacked image matrix as image similarity metric. To handle breathing motion discontinuities we use the isotropic total variation [7] regularization term $$$\|\nabla t_i\|_{2,1}$$$. In contrast to the squared L2 norm of displacements gradients used in [8], the TV norm does not penalize the sharpness of motion transitions. Eventually, image registration is formulated as the following optimization problem: $$\text{min}_{t_1,\dots,t_N}\sum_{i=1,\dots,N}\frac{\Sigma_{i,i}}{\sqrt{i}}+\lambda_\text{TV}\sum_{i=1,\dots,N}\|\nabla t_i\|_{2,1},\quad\quad(1)$$ where $$$U\Sigma V^T=[f_1\circ d(t_1)\dots f_N\circ d(t_N)]\in\mathbb{R}^{L\times N}$$$ is a singular value decomposition of the image stack. The regularization parameter $$$\lambda_\text{TV}$$$ controls the amount of spatial coherence and is tuned manually. As it was shown in [4], the optimal value of $$$\lambda_\text{TV}$$$ is robust among different image modalities. To solve the optimization problem (1) we employ a coarse-to-fine approach by constructing a Gaussian image pyramid. At each pyramid level the cost function (1) is minimized by the LBFGS based method [4] with approximated derivative of the nuclear norm: $$$U\text{diag}(1/\sqrt{1},\dots,1/\sqrt{N})V^T$$$.
Data analysis
For IVIM parameter regression, a modified segmented least-squares approach [9] was used. The signal $$$S(b)$$$ was fitted using the IVIM model: $$S(b)=S_0\left(f\exp(−bD^\ast)+(1−f)\exp(−bD)\right),\quad\quad(2)$$ where $$$S_0$$$ — reference intensity, $$$b$$$ — diffusion encoding strength, $$$D$$$ — diffusion coefficient, $$$f$$$ — perfusion fraction, $$$D^\ast$$$ — pseudo-diffusion coefficient.
The regularization parameter $$$\lambda_\text{TV}$$$ was set to 0.025. For reference, groupwise registration as implemented in the Elastix [5] and pairwise registration with bending energy regularization as implemented in the NiftyReg [8] was performed. The B-spline grid spacing for all methods was set to 4 pixels. A total of three datasets from healthy volunteers were evaluated.
Results
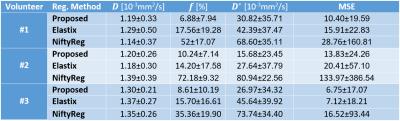
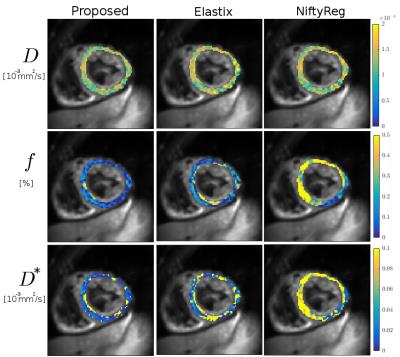
Registration run-times were as follows: 4min for the proposed method, 54min for Elastix, 12min for NiftyReg. An example of registration is visualized in Figure 2. IVIM parameters maps estimated using model (2) for volunteer #3 are shown in Figure 3. Numerical parameter estimates are reported in Table 1. The proposed method was found to improve the mean squared IVIM model residual by 24% and 71% compared to Elastix and NiftyReg registrations, respectively.Discussion
Visual inspection of displacement fields as shown in Figure 2 reveals that NiftyReg tends to oversmooth transformation which results in high IVIM parameters uncertainty. The results indicate that the proposed registration provides smaller standard deviation of IVIM parameters for most of the cases. Figure 3 also shows more homogeneous parameter maps estimated with the proposed method. IVIM parameters derived with the proposed method are within the expected range. Besides its accuracy, the high efficiency of the proposed method enables exhaustive testing on consumer level machines.Conclusion
Acknowledgements
The authors acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 668039.References
[1] Le Bihan D. Intravoxel incoherent motion imaging using steady-state free precession. Magnetic Resonance in Medicine. 1988;7(3):346-51.
[2] Moulin K, Croisille P, Feiweier T, et al. In vivo free-breathing DTI & IVIM of the whole human heart using a real-time slice-followed SE-EPI navigator-based sequence: a reproducibility study in healthy volunteers. Journal of Cardiovascular Magnetic Resonance. 2015;17(1):1.
[3] Delattre BM, Viallon M, Wei H, et al. In vivo cardiac diffusion-weighted magnetic resonance imaging: quantification of normal perfusion and diffusion coefficients with intravoxel incoherent motion imaging. Investigative Radiology. 2012;47(11):662-70.
[4] Vishnevskiy V, Gass T, Szekely G, Tanner C, Goksel O. Isotropic Total Variation Regularization of Displacements in Parametric Image Registration. IEEE Transactions on Medical Imaging. 2016. Preprint.
[5] Huizinga W, Poot DH, Guyader JM, et al. PCA-based groupwise image registration for quantitative MRI. Medical Image Analysis. 2016;29:65-78.
[6] Stoeck CT, Von Deuster C, Genet M, Atkinson D, Kozerke S. Second-order motion-compensated spin echo diffusion tensor imaging of the human heart. Magnetic Resonance in Medicine. 2015;75(4).
[7] Blomgren P, Chan TF. Color TV: total variation methods for restoration of vector-valued images. IEEE Transactions on Image Processing. 1998;7(3):304-9.
[8] Rueckert D, Sonoda LI, Hayes C, Hill DL, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Transactions on Medical Imaging. 1999;18(8):712-21.
[9] Notohamiprodjo M, Chandarana H, Mikheev A, et al. Combined intravoxel incoherent motion and diffusion tensor imaging of renal diffusion and flow anisotropy. Magnetic Resonance in Medicine. 2015;73(4):1526-32.
Figures