Synopsis

Golden angle radial sampling allows for flexible sliding window reconstructions while minimizing motion sensitivity and undersampling artifacts. Simultaneous MultiSlice (SMS) can be used to increase the spatial coverage without decreasing the framerate. Here we show that the golden angle profile ordering is in principle not compatible with the in-plane phase cycling scheme required by SMS. It follows that these are only compatible for a certain number of spokes, namely when the number of spokes is part of the Fibonacci sequence and the SMS factor is a divisor of this number.

Purpose

Golden Angle (GA) radial sampling is attractive for use in MR therapy guidance, because of its insensitivity to motion, benign undersampling artefacts, and flexible reconstruction window in sliding window reconstructions [1]. It has been demonstrated that radial sampling can be be combined with Simultaneous Multi-Slice (SMS) [2,3], but it is not evident that the GA profile ordering will always result in the required in-plane phase cycling pattern. Here, we will derive a phase cycling prescription that fulfills the requirement [2] that neighboring profiles can be made to add constructively for one slice only, while interfering destructively for the others, and evaluate its efficacy using simulations.

Theory

GA radial encoding collects k-space profiles sequentially, with increments of the profile azimuthal angle $$$ϑ$$$ of $$$φπ≈111.25°$$$. Here, $$$φ≡(√5-1)/2$$$ such that $$$φ^2=1-φ$$$. The GA radial scheme is tightly connected to the Fibonacci series, $$$Fib(1)=1$$$, $$$Fib(2)=1$$$, $$$Fib(n)=Fib(n-1)+Fib(n-2)$$$, and for a total number of profiles $$$N=Fib(n)$$$, a nearly uniform profile distribution is obtained.

For k-space filling using full echoes, we are interested in the distribution of the ϑ acquired on a semicircle from 0 to π radians, i.e. the value of $$$ϑ=(mφ)_{mod1}$$$. It can be shown that $$((m+Fib(n))φ)_{mod1}=(mφ)_{mod1}+φ^n(-1)^{n-1}\>Eq.1$$ If $$$N=Fib(n)$$$, the profile ordering has two sizes of azimuthal gaps Δϑ [1], viz. $$$Δϑ_1=φ^{n-1}$$$ and $$$Δϑ_2=φ^{n-2}$$$. As can be seen from Eq.1, these gaps occur for pairs $$$1\leq m_1,m_2\leq Fib(n)$$$ such that $$m_2-m_1=\pm Fib(n-1)\RightarrowΔϑ=\pmφ^{n-1}(-1)^{n}$$ $$m_2-m_1=\pm Fib(n-2)\RightarrowΔϑ=\mpφ^{n-2}(-1)^{n}$$For brevity, and without loss of generality, assume $$$n$$$ even and evaluate the neighbors of a profile $$$m_1φ_{mod1}$$$ in positive sense. We then have two possible cases: $$\begin{cases}m_1\leq Fib(n-2) \Rightarrow m_2=m_1+Fib(n-1)\leq Fib(n) \Rightarrow Δϑ=φ^{n-1}\\m_1> Fib(n-2) \Rightarrow 1\leq m_2=m_1-Fib(n-2)\leq Fib(n-1) \Rightarrow Δϑ=φ^{n-2}\end{cases}\>Eq.2$$ thus tracing the neighbors of a profile involves stepping through $$$m$$$ by increments of Fib(n-1) or decrements of Fib(n-2).

Radial SMS works by exciting multiple slices simultaneously with a MultiBand (MB) pulse, while cycling the relative signal phase between these slices. Suppose we have a sequence with simultaneous multislice (SMS) factor P and $$$PQ=Fib(n)$$$, requiring P different phase shifts, which are incremented with every profile. Then profiles with index $$$m=(q-1)P+p$$$ at angle $$$ϑ=mφπ$$$ are grouped as: $$\begin{matrix} 1&P+1&(q-1)P+1&…&(Q-1)P+1\\ 2&P+2&(q-1)P+2&…&(Q-1)P+2\\ p&P+q&(q-1)P+q&…&(Q-1)P+q\\ \vdots&\vdots&\vdots&&\vdots\\ P&2P&qP&…&PQ& \end{matrix}$$ For optimal incoherence[2], each phase shift should be represented in every set of P neighboring profiles, i.e. every P-th profile is from the same row, but all others are from different rows. From Eq.2 we may write the indices $$$m_i$$$ of the i-th neighbor of $$$m_0$$$ as: $$m_i=m_0+k_+Fib(n-1)-k_-Fib(n-2)\\=m_0+(k_++k_-)Fib(n-1)-k_-Fib(n)$$with $$$k_+$$$ and $$$k_-$$$ the numbers of increments and decrements respectively. But since $$$Fib(n)=PQ$$$ and since the greatest common divider of Fib(n) and Fib(n-1) is 1, $$$m_i$$$ and $$$m_0$$$ can be from the same row if and only if $$$k_++k_- $$$ is a multiple of P. From Eq.1 it also follows that $$$mφ$$$ nearly coincides with $$$mφ+Fib(n)$$$ thus ensuring that the sliding window reconstruction of Fib(n) profiles can be maintained.

Methods

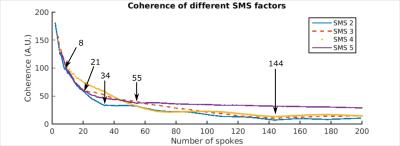
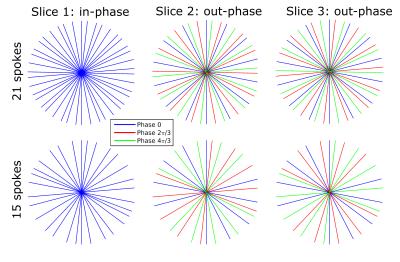
In simulations, the influence of the number of spokes N per frame N on the phase cycling patterns and incoherence was analyzed. An analytical software phantom was used to generate k-space data for SMS factors 2-5. The phase of sequential spokes was cycled with (0, π), (0, 2π/3, 4π/3), (0, π/2, π, 3π/4), and (0, 2π/5,…,4π/5) for each slice, respectively. This way the first slice was in-phase, while the other slices were out-of-phase and showed noise in the image [2] (fig. 1). Coherence of the out-of-phase slices was quantified by the L1 norm after applying a mask obtained from the coherent image. Low values signify high incoherence, and hence a small amount of signal leakage into the in-phase slice. Simulations were performed in MATLAB using a NUFFT toolbox [4].

Results and Discussion

Simulations of the coherence as a function of the number of spokes show that the coherence of the second slice is minimal when $$$N=Fib(n)$$$ and the SMS factor (i.e. P, the number of phase cycles) divides the N (fig. 2,3). For SMS 2 we see local minima at 8, 34, and 144 spokes, for SMS 3 at 21 and 144 spokes, for SMS 4 at 144 spokes, and for SMS 5 at 55 spokes. These results are in accordance with the derivations outlaid in the theory section.

Conclusion

Acknowledgements

References

[1] Winkelmann S et al., IEEE Trans Med Imaging 26, 2007

[2] Yutzy SR et al., MRM 65(6), 2011

[3] Cloos, MA et al., Proceedings ISMRM abstract 0608, 2016

[4] Fessler JA, JMRI 188(2), 2007