5056
SUPER: a novel acquisition and reconstruction strategy for improved efficiency and resolution in parameter mapping1Yale University, New Haven, CT, United States
Synopsis
Standard parameter mapping methods such as T1 and T2 mapping suffer from long scan time and low resolution due to the need to sample multiple images along the relaxation curve. Here we propose a novel acquisition and reconstruction strategy to improve efficiency by undersampling each k-space frame in the phase-encoding direction. By shifting the undersampling pattern circularly in each time frame, the relaxation signal at spatially distinct voxels is modulated and combined into a single signal, which can be used to reconstruct the parameters by solving a small-size nonlinear equation. This technique is especially suitable for applications where multiple TIs or TEs are needed, and can improve either resolution or acquisition time.
Purpose
Parameter mapping (T1, T2, etc.) has been increasingly used in clinical MRI applications in recent years. However, standard parameter mapping methods require acquiring multiple images along the relaxation curve, causing prolonged scan time and suboptimal resolution. This is especially true for cardiac MRI applications, where scan time is also restricted by cardiac motion. In this work, we propose a novel acquisition and reconstruction strategy for parameter mapping to improve its efficiency and resolution. The method “SUPER”, representing “Shift Undersampling improves Parameter mapping Efficiency and Resolution”, undersamples k-space in the phase-encoding direction and reconstructs the parameters from the aliased images based on the parameter models. The reduced time can be traded-off for a higher resolution. We demonstrate this technique with simulations and in vivo MOLLI (1), which is the standard cardiac T1 mapping method.Methods
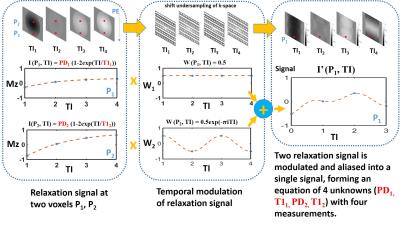
Figure 1 illustrates the basic idea of SUPER through a 2-FOLD accelerated T1 mapping. K-space acquired at each TI is undersampled in the phase-encoding direction, with the undersampling pattern circularly shifted by one unit in the subsequent k-space. After Fourier transform of the undersampled k-space, the signal at each voxel is equal to a summation of two relaxation signal, one of which is modulated at a different frequency. Since the relaxation has a known model, the model parameters can be estimated by solving the equation that has four unknowns and four measurements at four TIs.
Consider a general T1 mapping application where an arbitrary undersampling factor, denoted by G, is used. The signal time series representing the T1 relaxation at voxel $$$n$$$ is $$$I(n, t_l) = A_n - B_ne^{-t_l/T_{1_n}}$$$, where $$$A_n$$$, $$$B_n$$$, and $$$T_{1_n}$$$ are the model parameters, and $$$n$$$ indicates a pixel location. After undersampling and Fourier transform, the resulting signal time series at voxel $$$n$$$ is $$$I'(n,t_l)$$$, and has aliasing. Due to the shift in undersampling pattern with time, the parameter values at voxel $$$n$$$ ($$$A_n$$$, $$$B_n$$$, $$$T_{1_n}$$$, etc) that control the original relaxation curves can be reconstructed by solving the equation that combines the multiple relaxation curves, as given below:
$$$I'(n,t_l) = \sum_{g=1-G/2}^{G/2} w(g,l) I(n - g\frac{FOV}{G}, t_l)$$$
where $$$l=0,1,\ldots, L-1$$$ indexes the acquisition time ($$$t_l$$$) of each image and w represents the temporal modulation function:
$$$w(g, l) = \frac{1}{G}e^{-j2\pi\frac{lg}{G}}$$$
Similar analysis concerning the temporal modulation has been described (2). The equation is solved for totally FOV/G lines in the phase-encoding direction ($$$n=0,1,\ldots, FOV/G-1$$$) to cover the entire image domain. The equation is solvable as long as number of time points L is larger than G multiplied by the number of parameter models. If only a few images are acquired along the relaxation curve, SUPER is not applicable; however, if the number of images is much larger than number of parameters, SUPER can significantly reduce the acquisition time.
SUPER was tested for T1 mapping. All imaging was performed on a 3T Siemens scanner. Phantom imaging used spin echo inversion recovery with 8 TIs. A T1 phantom with T1s ranging from 200ms to 550ms was imaged, and the T1 map was generated with full k-space data and undersampled k-space by using 2-fold and 4-fold SUPER. The scan parameters for the phantom study was FOV =240mm x 240 mm, FA 90°, image size 192x192, and BW 130Hz/Pixel. In healthy subjects, we performed a standard MOLLI and reconstructed with the standard approach and 2-fold SUPER approach. A modified 2-fold SUPER-MOLLI sequence with doubled phase-encoding resolution compared to MOLLI but an identical acquisition time within the cardiac cycle was also performed. Sequence parameters were: FOV 360x280, acquisition pattern: 3-3-5, RR=1000ms, the three smallest TIs: 100ms, 200ms, and 350ms, image size: 192x72 (MOLLI) and 192x144 (SUPER-MOLLI).
Results
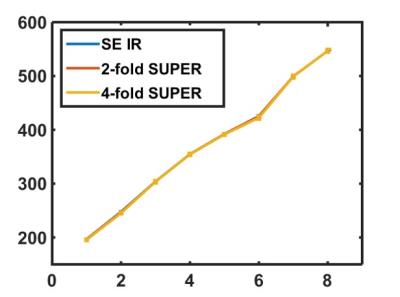
Figure 2 shows phantom results for T1 mapping with standard reconstruction, 2-fold SUPER, and 4-fold SUPER. Figure 3 shows the T1 estimates of the 8 T1 standards from the three methods. Figure 4 shows the MOLLI image, the SUPER-MOLLI image reconstructed with 2-fold undersampling, and the high-resolution SUPER-MOLLI image. The average T1 from MOLLI, SUPER-MOLLI, and high-resolution SUPER-MOLLI are 1139±73ms, 1117±71ms, and 1148±61ms for myocardium, 1692±49ms, 1688±55ms, and 1710±68ms for blood pool, respectively. The higher resolution SUPER MOLLI (with no increase in acquisition time) greatly improves the T1 map, compared to lower resolution MOLLI.Conclusions
We demonstrate a novel technique for accelerating parameter mapping. This technique is especially suitable for applications where multiple TIs or TEs are needed, and requires only minor sequence modifications. The technique can be combined with other accelerations such as parallel imaging, and can improve either resolution or acquisition time.Acknowledgements
No acknowledgement found.References
1. Messroghli DR, MRM 2004, 2. Madore B, MRM 1999Figures