5050
Simultaneous interleaved blip up/down readout for dynamic off-resonance correction in functional EPI1Stanford University, Stanford, CA, United States
Synopsis
Motion and geometric distortions of EPI acquisitions remain challenging as motion during an fMRI scan affects the stability of the time series in two ways: Rigid motion displaces voxels by “moving” the spins. A change in head orientation and the complex interplay of external and internal susceptibility differences lead to a change in the off-resonance field. In combination with an EPI readout this change in off-resonance field leads to an “apparent” voxel displacement. Here, we propose the simultaneous acquisition of a blip-down navigator with the original blip-up host-EPI sequence which is used to derive a snapshot of dynamic off-resonance changes.
Introduction
Geometric distortions of EPI acquisitions remain challenging especially for high-field applications or in the case of strong off-resonance fields. Subject head motion during an fMRI scan affects the stability of the time series in two ways: 1) Rigid body motion displaces voxels by actual movement. 2) A change in head orientation and the complex interplay of external and internal susceptibility differences lead to a change in the off-resonance field. In combination with an EPI readout, this change in off-resonance field leads to an “apparent” voxel displacement. Prospective motion correction allows for correction of the rigid component, but dynamic changes of the fieldmap remain a source for artifacts. Here, we propose the simultaneous acquisition of a blip-down navigator within the original blip-up host-EPI sequence. The navigator and the host-EPI sequence then have opposite geometric distortions (voxel stretching <-> compression). Using image processing it is possible to derive an off-resonance map from the low resolution blip-down navigator and the host-EPI sequence. If both, the navigator and the host sequence are accelerated, one can choose the sampling pattern in a way that the navigator fills in missing k-space samples. By performing a joint off-resonance corrected hybrid-SENSE reconstruction (1) the g-factor penalty is reduced because of the higher sampling density in k-space.Theory
Ignoring off-resonance effects along the readout direction, and performing an FT along the $$$k_x$$$ domain, transforms the k-space data $$$s_0(k_x,k_y,k_z)$$$ to an hybrid space $$$ s(x,k_y,k_z) $$$. For every position $$$ x=x_n$$$ we can write the signal equation (forward model) in matrix notation as $${\bf s=Fm} \hspace{1cm} [1]$$ with the unknown magnetization $$$ {\bf m} \in \mathbb{C}^{N_yN_x \times 1} $$$ and the signal vector $$$ {\bf s} \in \mathbb{C}^{N_sN_c \times 1} $$$ that consists of all $$$N_s$$$ acquired k-space samples times the number of receiver coils $$$N_c$$$. The effective encoding matrix $$$ \bf F $$$ models phase effects due to gradient encoding and off-resonance contributions. In order to invert the rectangular matrix $$$\bf F$$$, we use a truncated singular value decomposition approach (TSVD) (2) where we completely suppress contributions from eigenvalues below a certain threshold $$$\lambda$$$. The solution is then given as $${ \bf m = F}_{pinv}^{reg}{\bf s} \hspace{1cm} [2]$$ For the joint blip up/down reconstruction we rewrite the signal model as $${\bf F_{\uparrow \downarrow}}=\left(\begin{array}{c}{\bf F_{\uparrow}}\\ {\bf F_{\downarrow}}\end{array}\right) \hspace{1cm} [3] $$ where $$$\bf F_{\uparrow}$$$ and $$$\bf F_{\downarrow}$$$ are the effective encoding matrices for the blip up and down trajectories. Noise enhancement maps (g-factor) are calculated as $$ g=diag(\sqrt{\frac{{\bf F}_{pinv}^{reg}({\bf F}_{pinv}^{reg})^T}{{\bf C C}^T} })/\sqrt{R_{tot}}$$Methods
Measurements were performed at 3T using an 8-channel head coil array. All reconstructions are performed off-line using MatLab. The “blip down navigated”-EPI acquisition is implemented by concatenating the blip-down navigator-EPI and the original EPI-acquisition while continuously playing out the EPI readout train (see Figure 1). The resolution of the blip-down navigator was fixed to Nnav=64 and the same in-plane acceleration Ry=2 was used for both acquisitions. The following acquisition parameters were used: FOV=22x22cm, NxxNy=128x128, Ry=2; partial Fourier=0.75, esp=0.55ms, slice thickness=2mm, TR=3s. The host-EPI and the navigator-EPI were reconstructed separately and a fieldmap was estimated using FSL 5.0’s topup ( http://fsl.fmrib.ox.ac.uk/fsl ) function with default parameters (3).Results
Figure 3 displays separate reconstruction of the navigator (a) and the host sequence (b). The white arrow indicates the phase encoding direction (up or down). Uncorrected, both reconstruction experience geometric distortions in opposing directions relative to the red lines that mark anatomical features of the image.
Performing an off-resonance corrected hybrid-SENSE reconstruction significantly reduces distortions and brings the navigator (d) and the full readout (e) into the same undistorted space that allows for a joint reconstruction (h) with reduced g-factor penalty (g).
Discussion
We have shown that it is feasible to acquire a blip-down navigator and the full resolution image in one continuous readout without significantly prolonging the acquisition time. The duration of the navigator is on the order of 10ms which means we can neglect motion effects between both readouts. This allows for a snapshot of the dynamically changing off-resonance field in case of head motion or breathing fluctuations In contrast to methods that rely on the phase to estimate off-resonance changes, the blip up-down approach is not affected by flow or CSF pulsatility that can lead to erroneous phase estimations and thus incorrect off-resonance changes. The joint reconstruction has the additional benefit of reducing the g-factor penalty in a parallel imaging reconstruction.Acknowledgements
NIH (2R01 EB002711 , 5R01 EB008706, 5R01 EB011654), the Center of Advanced MR Technology at Stanford (P41 RR009784), Lucas Foundation.References
1. Zhu K, Dougherty R, Wu H, Middione M, Takahashi A, Zhang T, Pauly J, Kerr A. Hybrid-Space SENSE Reconstruction for Simultaneous Multi-Slice MRI. IEEE Trans. Med. Imaging [Internet] 2016. doi: 10.1109/TMI.2016.2531635. 2. Hansen PC. Truncated Singular Value Decomposition Solutions to Discrete Ill-Posed Problems with Ill-Determined Numerical Rank. SIAM J. Sci. Stat. Comput. [Internet] 1990;11:503–518. doi: 10.1137/0911028. 3. Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. Neuroimage 2004;23 Suppl 1:S208-19. doi: 10.1016/j.neuroimage.2004.07.051.Figures
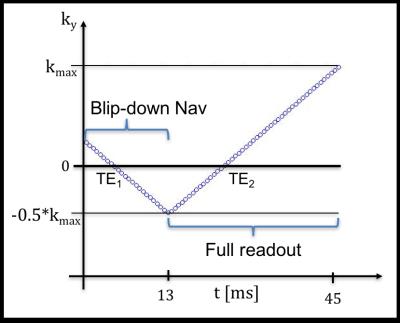
Figure 1:
Blip-down navigator and blip-up host-EPI in a single continuous readout. 6/8 Partial Fourier sampling and 2x in-plane acceleration is employed for the navigator and the full readout.
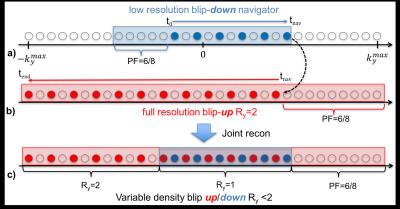
Figure 2 :
Interleaved navigator and host-EPI sampling patterns for 2x in-plane acceleration. a) Low resolution blip-down navigator. b) Full blip-up acquisitions shifted by one k-space sample relativ to the navigator. c) Combined (joint) sampling patterns with higher density sampling in the center of k-space.
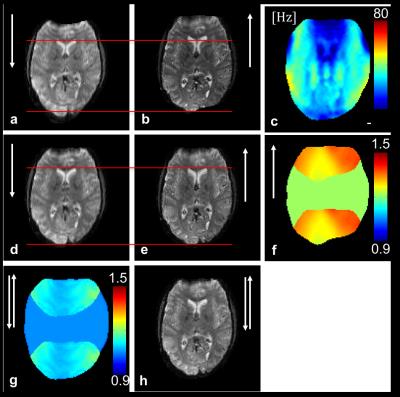
Figure 3:
The uncorrected blip-down navigator (a) and the full-resolution blip-up EPI (b) display geometric distortions in opposing directions. The fieldmap in Hz generated from a and b using FSL’s topup function is displayed in c. Off-resonance corrected hybrid-SENSE reconstruction for the navigator (d) and the host-EPI (e). Because the undersampling pattern is identical for both acquisitions, they share a common noise enhancement (g-factor) map in f. Joint navigator and host-EPI reconstruction (h) displays increased SNR due to averaging less g-factor penalty (as displayed in g).