5028
Lipid Suppression Around Metal Implants Using a B1-Optimized Adiabatic Inversion Pulse1MR Applications and Workflow, GE Healthcare, Waukesha, WI, United States, 2MR Systems Engineering, GE Healthcare, Waukesha, WI, United States, 3Radiology, Medical College of Wisconsin, Milwaukee, WI, United States
Synopsis
A nonlinear iterative optimization algorithm was used to design an adiabatic inversion pulse with a bandwidth of 3.2 kHz. With a larger bandwidth, the new pulse maintains the same SAR as the original inversion pulse and also has an improved spectral profile. Images obtained on a phantom, and in-vivo, show improved fat suppression, and reduced ripple artifacts in the slice domain. In addition to improving image quality, the optimized RF pulse may improve the diagnostic ability of STIR with 3D multi spectral imaging.
Introduction
Conventional magnetic resonance imaging sequences are severely hampered in the presence of high susceptibility metallic implants. This limitation has been overcome using 3D-multi spectral imaging sequences (3D-MSI) such as MAVRIC SL1 and SEMAC2. While conventional contrasts such PD, T13, T24, and even diffusion weighting5 have been shown to be feasible around metal implants, fat suppression using phase based approaches has been extremely difficult to accomplish. Even in the presence of advanced phase processing6, Dixon based approaches will show fat water swaps close to the implant surface which should be avoided. Hence, fat suppression around metal has taken advantage of the T1 differences between fat and water, using the Short Tau Inversion Recovery (STIR) sequence. The quality of these STIR images relies heavily on the quality of the inversion pulse. The work presented here seeks to optimize the spectral quality of the adiabatic inversion pulse using an iterative Fourier series based optimization approach. The optimization also seeks to increase RF bandwidth of the pulse, while having no impact on the SAR.Methods
The original pulse is a 16 ms adiabatic inversion pulse, with a dwell time of 40 μs, a FWHM of 2400 Hz, with a nominal flip angle of 200°, and a peak b1 of 12.18 μT. For the optimization algorithm, a hyperbolic secant pulse with a similar duration and dwell time was chosen as the initial condition. Its RF bandwidth was chosen to be equal to that of the slice selective pulse (3200 Hz). This pulse was Fourier transformed, and 130 Fourier coefficients (65 real, 65 imaginary) were chosen for optimization. These coefficients were tested in a Bloch simulation at 3 RF amplitudes (B1, B1+25%, B1+50%; B1 = 17μT) to test its adiabatic performance. These numbers were used to evaluate a cost function χ
$$$\chi=\sum_0^f(\theta_{B1,A1}-\theta_{Ideal})^{2} + \sum_0^f(\theta_{B1,A2}-\theta_{Ideal})^{2} + \sum_0^f(\theta_{B1,A3}-\theta_{Ideal})^{2} + \lambda_{1}|B_{1,peak}| + \lambda_{2}\sum_0^NB_1^2$$$
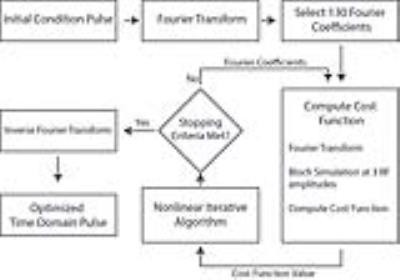
where the first 3 terms represent the Bloch simulation evaluation at 3 RF amplitudes, f is the number of points in the spectral domain, N in the time domain. and were empirically determined to be 1000, and 50 respectively. This cost function information was used in a nonlinear optimization routine that updated the Fourier coefficients. Post convergence, the Fourier coefficients were used to generate the time domain RF pulse. The algorithm is summarized in Figure 1.
The performance of the RF pulse was first tested using a prototype MAVRIC SL sequence in a fat-water phantom with a hip implant. The RF pulse was also tested on human volunteers. Written, informed consent was obtained prior to image acquisition, and the study was approved by the local institutional review board.
Results
Figure 2 compares the spectral performance of the original and optimized pulses. Compared to the initial condition pulse, the optimized inversion pulse has significantly lower peak b1 (23 μT Vs 18.4 μT), and retains the cleaner spectral profile of the initial condition. Figure 3 shows STIR images obtained in a fat-water phantom with a Co/Cr hip implant. While the 2D-FSE are heavily warped, both 3D-MSI images accurately delineate the implant boundary. The optimized inversion pulse shows a 60% improvement in fat suppression, and no banding artifacts in the slice dimension. The pulses showed similar performance when imaging the the human volunteer (Figure 4). Compared to the 2D FSE images, the 3D MSI images show no artifacts, and the optimized pulse has a better fat suppression, and no ripple artifacts in the slice domain.Discussion and Conclusions
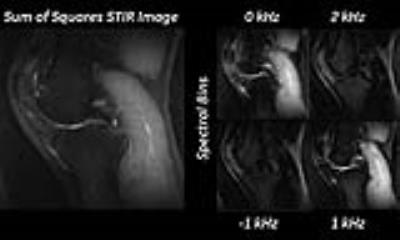
Compared to recursive approaches used before7, the Fourier based approach to optimization lent itself more naturally to optimizing the inversion pulse. While the fat suppression of 2D FSE is superior, the fat suppression in 3D MSI is limited by its need to cover multiple frequencies. This is demonstrated in figure 5. While the on resonance spectral-bin has excellent fat suppression, as we move further off resonance, the RF power applied to the fat and water frequencies are lower, increasing the relative T1 recovery. Thus when the bins are combined, the effective fat suppression is lowered. The optimized inversion pulses provide a dramatic improvement in image quality, and fat suppression. Also, the newer pulses help reduce bin-combination artifacts, which are often seen in the slab-selective dimension. This original source of artifact arose from the lower bandwidth of the original inversion pulse, which led to incomplete inversion of frequencies at the edge of the refocusing pulse. While retaining the same SAR, the larger bandwidth of the optimized pulse helped cover a larger portion of the refocusing bandwidth, leading to fewer non inverted frequencies (figure 2B).Acknowledgements
No acknowledgement found.References
1) Koch et al., Imaging near metal with a MAVRIC-SEMAC hybrid. Magn Reson Med. 2011;65(1):71-82
2) Lu et al., SEMAC: Slice encoding for metal artifact correction in MRI. Magn Reson Med. 2009;62(1):66-76.
3) Koch et al., Flexible longitudinal magnetization contrast in spectrally overlapped 3D-MSI metal artifact reduction sequences: Technical considerations and clinical impact. Magn. Reson. Med., 74: 1349–1355.
4) Yoon et al., T2-weighted Multispectral Imaging for Postoperative Imaging of Patients with Lumbar Spinal Fusion, In: Proc. Intl. Soc. Mag. Reson. Med. Singapore; 2016:2260.
5) Kaushik et al., Clinically Viable Diffusion-Weighted Imaging Near Metal using 2D-MSI PROPELLER DUO, In: Proc. Intl. Soc. Mag. Reson. Med. Singapore; 2016:370.
6) King et al., Path based phase estimation for fat suppression near metal implants. In: Proc. Intl. Soc. Mag. Reson. Med. Singapore; 2016:3268.
7) Garwood et al., The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153(2):155-177.
Figures