4927
Uniform flip angle 3D tailored excitation for MR breast imaging at 3T1Institute of Biomedical Engineering, National Taiwan University, Taipei, Taiwan, 2Medical Physics, Department of Radiology, University Medical Center Freiburg, Freiburg, Germany, 3Department of Neuroscience and Biomedical Engineering, Aalto University, Espoo, Finland
Synopsis
We proposed a two pulses excitation method using the linear gradients to achieve uniform 3D breast excitation. Different to previous studies, we don't need extra hardware and this method is applicable to all MRI systems. Compared to conventional excitation method, our method was able to achieve a more uniform flip angle (8.24% to 5.6%) and the mean flip angle difference between the left and the right breast was improved from 10.2% to 1.5%.
Target audience
Scientists and physician interest in uniform flip angle excitation for the breast imaging at high field MRI.Introduction
Dynamic contrast enhancement MRI (DCE-MRI) is a useful tool in breast cancer diagnosis. MRI at field strength higher than 3T may potential enhance signal-to-noise ratio, improve resolution, or shorten scanning time. However, due to the shorter wavelength of the magnetic resonance signal at a higher field strength, the inhomogeneous transmitted magnetic field (B1+) can seriously degrade breast images at 3T. At 3T breast MRI, the variation of the |B1+| is typically along the left-right direction, such that one side of the breast may reach a factor of 1.3 to 21, 2. The lower flip angle at one side of the breast can cause the enhancement rate of the lesion at 3T lower than the same lesion at 1.5T1, 3. This asymmetric contrast can cause difficulties in diagnosis, and limit acceptance of 3T for breast imaging. To reduce this artifact, the RF shimming technique2, 4 or the strategy of the breast with dielectric pads2 have been proposed to achieve more homogeneous B1+. However, these methods need extra hardware and may not suitable for all MR scanner. For brain imaging, several excitation methods were proposed to compensate for the central brightening |B1+| using the nonlinear spatial encoding magnetic field to achieve uniform flip angle excitation5-7. These methods required that the iso-contour of |B1+| is similar to the iso-contour of the spatial encoding magnetic field. For the left-right asymmetric distribution of B1+ in breast region, we hypothesize that similar method can be applied for breast imaging using linear gradient only. We proposed a 3D tailored excitation method and demonstrate this method can achieve more uniform flip angle through simulation using measured |B1+|.Methods
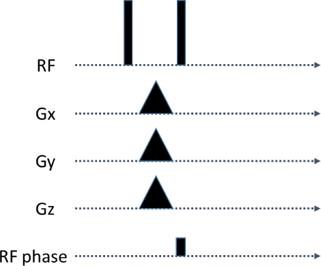
B1+ map was acquired using 3D gradient echo based Bloch-Siegert shift mapping8 (FOV=32x16x19cm, pixels=64x32x38, TE/TR=13/18ms, 8ms Fermi pulse). As tailored excitation method and SAGS5, 6, in order to achieve uniform flip angle $$$\theta $$$ =35o3, we used two RF pulses with flip angle $$$\alpha$$$, and linear gradients together with an added phase of the second pulse such that the phase between the first and the second excited transverse magnetization is $$$\phi \left ( x, y, z \right )=a_{0}+a_{1}x+a_{2}y+a_{3}z$$$ (Figure 1), where $$$a_{i}$$$ were optimized to achieve most uniform excitation based on the equation: $$a_{i}=argmin_{a_{i}'}\left \| \theta -acos(1-(cos(a_{0}+a_{1}x+a_{2}y+a_{3}z)+1)sin^{2}\alpha ) \right \|_{2}^{2}$$ This optimization problem was solved using quasi-Newton method. We used 4 different values of $$$\alpha $$$ such that the total RF power of these two pulses equals to 1, 2, 3 and 4 times of standard single pulse method with a mean flip angle equal 35o. The flip angle homogeneity was quantified by relative standard deviation, $$$E_{1}=\frac{std(\Psi(all))) }{mean(\Psi(all))}$$$, and mean difference between left and right breast, $$$E_{2}=\frac{abs(mean(\Psi(left))-mean(\Psi(right)))}{mean(\Psi(all))}$$$, where $$$\Psi$$$ denotes the flip angle map. One female volunteer data were collected on 3T MRI scanner (Prisma, Siemens).Results
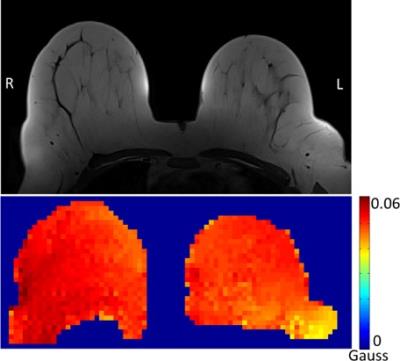
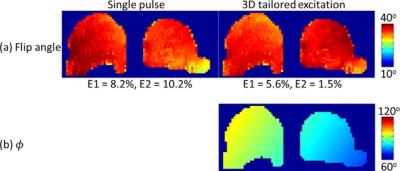
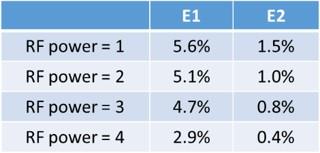
Figure 2 shows the center axial slice of the T1 weighted image and the measured |B1+|; the difference of |B1+| between left and right breast is about 10% of their averaged value. Figure 3a shows the flip angle of the center axial slice using the single pulse and our method with the same RF power. Figure 3b shows the phase that was induced by the linear gradient between two excitation pulses. The phase distribution has the same varying trend as |B1+| that was able to counteract |B1+| inhomogeneity and excite more uniform flip angle (E1=5.6%) than the single-pulse method (E1=8.2%). Furthermore, the difference of mean flip angle between left and right is reduced from 10.2% to 1.5%. Table 1 shows that the flip angle homogeneity can be improved by increasing the RF power.Discussion
Compared to the previous studies, our measured |B1+| map shows less variation between left and right breast. The variation may be subject- and system-dependent, however, we believe that the proposed method is able to provide a similar improvement ratio for other cases. The higher RF power can achieve more uniform flip angle; this trend can be explained by the theory of composite pulses9, which can achieve homogeneous excitation without using gradient field. We also can use nonlinear gradients for 3D tailored excitation method to achieve even more homogeneous flip angle. Simulation results using monoplanar gradient system10 together with linear gradient system can reduce the error further to E1=5.2%, 4.8%, 4.4% and 2.7% for 1, 2,3 and 4 times of single pulse RF power. We realized that our method is similar to k-t point method11, however, our proposed method is not only limited to small angle excitation.Acknowledgements
This work was partially supported by Ministry of Science and Technology, Taiwan (103-2628-B-002-002-MY3, 105-2221-E-002-104), and the Academy of Finland (No. 298131).References
1. Kuhl, C.K., et al., Effect of B1 inhomogeneity on breast MR imaging at 3.0 T. Radiology, 2007. 244(3): p. 929-930.
2. Winkler, S.A. and B.K. Rutt, Practical methods for improving B1+ homogeneity in 3 tesla breast imaging. Journal of Magnetic Resonance Imaging, 2015. 41(4): p. 992-999.
3. Azlan, C.A., et al., B1 transmission-field inhomogeneity and enhancement ratio errors in dynamic contrast-enhanced MRI (DCE-MRI) of the breast at 3T. Journal of Magnetic Resonance Imaging, 2010. 31(1): p. 234-239.
4. Rahbar, H., et al., Improved B1 homogeneity of 3 tesla breast MRI using dual-source parallel radiofrequency excitation. Journal of Magnetic Resonance Imaging, 2012. 35(5): p. 1222-1226.
5. Duan, Q., P. van Gelderen, and J. Duyn, Tailored excitation using nonlinear B0-shims. Magnetic resonance in medicine, 2012. 67(3): p. 601-608.
6. Hsu, Y.C., et al., Mitigate B1+ inhomogeneity using spatially selective radiofrequency excitation with generalized spatial encoding magnetic fields. Magnetic resonance in medicine, 2014. 71(4): p. 1458-1469.
7. Hsu, Y.C., et al., Mitigation of B1+ inhomogeneity using spatially selective excitation with jointly designed quadratic spatial encoding magnetic fields and RF shimming. Magnetic Resonance in Medicine, 2016.
8. Sacolick, L.I., et al., B1 mapping by Bloch-Siegert shift. Magnetic Resonance in Medicine, 2010. 63(5): p. 1315-1322.
9. Levitt, M.H., Composite pulses. 2007: Wiley Online Library.
10. Littin, S., et al., Monoplanar gradient system for imaging with nonlinear gradients. Magnetic Resonance Materials in Physics, Biology and Medicine, 2015. 28(5): p. 447-457.
11. Cloos, M., et al., kT-points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magnetic resonance in medicine, 2012. 67(1): p. 72-80.
Figures