4755
Non-rigid Groupwise Image Registration for Myocardial Strain Quantification from High-Resolution 3D Tagging1Institute for Biomedical Engineering, ETH Zurich, Zurich, Switzerland
Synopsis
Cardiac motion can be efficiently assessed using 3D-tagged MR sequences for diagnostic purposes. However, there is a lack of robust post-processing tools to derive regional motion and strain data. Current registration methods tend to underestimate radial strain in the left ventricle. In order to provide accurate strain estimates we leverage temporal smoothness of displacements and low-rank structure of aligned images. The herein proposed method is 38% more accurate for radial strain, 27% for circumferential strain and 25% for longitudinal strain estimation than state-of-the-art registration implemented in Elastix while increasing computational speed by a factor of six.
Introduction
Estimation of regional cardiac motion is crucial for assessing cardiac function. Moreover, strain data is of critical importance for biomechanical modelling of the heart. Available 3D image registration algorithms for processing MR cine and tagging data tend to underestimate peak myocardial radial strain values [1] and are computationally expensive.
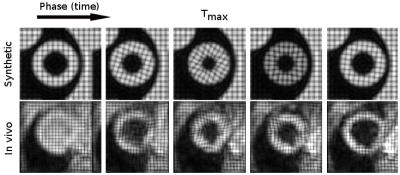
In this work we present a mask-free 3D image registration method based on a parametric total variation approach [2] to process high-resolution 3D tagging data. The approach is demonstrated to allow for sharp motion discontinuities that occur around myocardial edges. We adopt a principal component analysis (PCA)-based image similarity metric [3], which accounts for image irregularities, such as the blood pool signal as present in the first frames of 3D tagging data (Figure 1).
Methods
Data acquisition
Synthetic and in vivo datasets were used to assess the performance of the method (Figure 1). In vivo data consisted of three 3D stacks with orthogonal line tagging [4] (distance 5 mm) acquired on a 1.5T clinical MR system (Philips Healthcare, Best, The Netherlands) equipped with a 32-channel cardiac receiver array during navigator gated free breathing (gating window 5 mm). Imaging parameters were as follows: spatial resolution: 2.5×5×5 mm3, temporal resolution: 24 ms, scan duration 2 min. Complementary spatial modulation of magnetization [5] was used to avoid tagline fading. Synthetic data was generated using realistic strain values [1].
Registration algorithm
Let $$$f^j_i (i=1,\dots, N, j=1,2,3)$$$ be $$$N$$$ 3D images corresponding to sequential cardiac phases and 3 tagging directions. For each image $$$f_i^j$$$ a displacement field $$$d(t_i)$$$ is parametrized by 1st order B-splines [6] with coefficients $$$t_i$$$. Assuming that aligned images $$$f^j_i\circ d(t_i)$$$ are linearly dependent, we estimate displacement fields by minimizing weighted nuclear norm of the stacked warped image matrix:
$$\text{min}_{t_1,\dots,t_N} \sum_{j=1,2,3}\sum_{i=1,\dots N}\frac{\Sigma^j_{i,i}}{\sqrt{i}}+\lambda_\text{TV}\sum_{i=1,\dots,N}\|\nabla t_i\|_{2,1}+\lambda_\text{time}\|D_2[t_1\dots t_N]\|_2^2,\quad(1)$$
where $$$U^j\Sigma^j (V^j)^T=[f^j_1\circ d(t_1)\dots f^j_N\circ d(t_N)]\in\mathbb{R}^{L\times N}$$$ is a singular value decomposition of the warped image stack and $$$L$$$ is number of pixels in each image. Isotropic total variation [7] regularization term $$$\|\nabla t_i\|_{2,1}$$$ encourages spatial coherence of displacement fields in spatial domain and $$$\|D_2[t_1\dots t_N]\|_2^2$$$ is the temporal smoothness penalty with $$$D_2$$$ being the second order finite difference operator. Regularization parameters $$$\lambda_\text{TV}$$$ and $$$\lambda_\text{time}$$$ control the amount of spatial and temporal smoothness respectively and are tuned manually. As reported in [2], optimal values of regularization parameters are robust among different anatomies and image modalities once the image similarity metric is fixed. The optimization problem (1) is solved by constructing a multiresolution image pyramids with the LBFGS based method, developed in [2] and approximate derivative of the nuclear norm as $$$U^j\text{diag}(1/\sqrt{1},\dots,1/\sqrt{N})(V^j)^T$$$.
Data analysis
The proposed registration method was compared to groupwise PCA-based registration implemented in the “Elastix” package [3] and 3D sine wave modeling (SinMod) [8]. B-spline grid spacing for the proposed and the Elastix registration methods was set to 4 pixels, $$$\lambda_\text{TV}=3.6\cdot10^{-6}$$$ and $$$\lambda_\text{time}=1.8\cdot10^{-7}$$$ based on synthetic data. Radial, circumferential and longitudinal vectors that define the local anatomical basis $$$R$$$ were calculated upon manual segmentation of the left ventricle. The Cartesian strain tensor $$$E_c=\frac12(F^TF-I)$$$ and polar strain tensor $$$E_p=R^TE_cR$$$ were computed using the Jacobian of the transformation field $$$F$$$ and radial, circumferential and longitudinal strains were derived.
The proposed method was implemented in Matlab.
Results
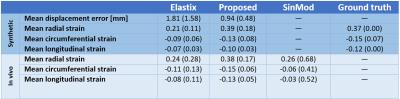
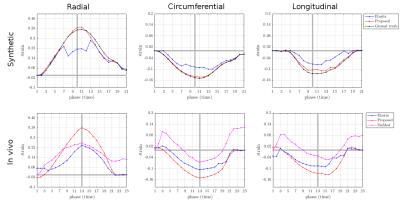
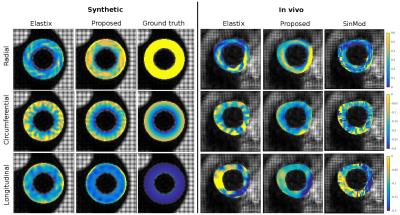
The computational time of the proposed registration method was 12 minutes (6-core Intel Core i7 CPU) compared to Elastix’s run time of 76 minutes. The mean Euclidean displacement error of the proposed method evaluated inside the myocardium over all cardiac phases was 0.94+/-0.48 mm on the synthetic data after comparing the resulting displacement field with the ground truth. Radial strain values at maximum contraction phase were 39% and 38% in synthetic and in vivo experiments respectively. Average strain values for both experiments are reported in Table 1 and Figure 2. Estimated strain maps are visualized in Figure 3.Discussion
The proposed method provides more accurate displacement estimates both in terms of transformation error and strain values, comparing to state-of-the-art Elastix registration [3]. For in vivo experiments estimated strains were closer to expected [1, 9, 10] values of 40% radial, -17% circumferential, -15% longitudinal with smaller standard deviation. Figure 2 shows that our registration method allows to consistently estimate radial strain at end systolic phase. In addition, the high efficiency of our method (~6 times faster than Elastix) enables exhaustive testing on consumer level machines and promises application of strain analysis in a clinical setting.Conclusion
In this work we have developed a method for accurate 3D-tagged data registration that is able to capture radial strain in the myocardium with increased accuracy compared to previously reported approaches.Acknowledgements
The authors acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No 668039.References
[1] Tobon-Gomez C, De Craene M, Mcleod K, et al. Benchmarking framework for myocardial tracking and deformation algorithms: An open access database. Medical Image Analysis. 2013;17(6):632-48.
[2] Vishnevskiy V, Gass T, Szekely G, Tanner C, Goksel O. Isotropic Total Variation Regularization of Displacements in Parametric Image Registration. IEEE Transactions on Medical Imaging. 2016. Preprint.
[3] Huizinga W, Poot DH, Guyader JM, et al. PCA-based groupwise image registration for quantitative MRI. Medical Image Analysis. 2016;29:65-78.
[4] Rutz AK, Ryf S, Plein S, Boesiger P, Kozerke S. Accelerated whole-heart 3D CSPAMM for myocardial motion quantification. Magnetic Resonance in Medicine. 2008;59(4):755-63.
[5] Fischer SE, McKinnon GC, Maier SE, Boesiger P. Improved myocardial tagging contrast. Magnetic Resonance in Medicine. 1993;30(2):191-200.
[6] Rueckert D, Sonoda LI, Hayes C, Hill DL, Leach MO, Hawkes DJ. Nonrigid registration using free-form deformations: application to breast MR images. IEEE Transactions on Medical Imaging. 1999;18(8):712-21.
[7] Blomgren P, Chan TF. Color TV: total variation methods for restoration of vector-valued images. IEEE Transactions on Image Processing. 1998;7(3):304-9.
[8] Wang H, Stoeck CT, Kozerke S, Amini AA. Analysis of 3D cardiac deformations with 3D SinMod. IEEE EMBC. 2013: 4386-4389).
[9] Zhong X, Spottiswoode BS, Meyer CH, Kramer CM, Epstein FH. Imaging three-dimensional myocardial mechanics using navigator-gated volumetric spiral cine DENSE MRI. Magnetic Resonance in Medicine. 2010;64(4):1089-97.
[10] Moore C, Lugo-Olivieri C, McVeigh E, Zerhouni E. Three-dimensional systolic strain patterns in the normal human left ventricle: characterization with tagged mr imaging. Radiology. 2000; 214(2):453-66.
Figures