Introduction

There is increasing interest in understanding the mechanical properties of human brain tissue and their influence on the formation of cortical folding during development or in pathological conditions such as traumatic brain injury^1,2. In myocardial tissue or muscle collagen and muscle fibers are structurally supporting the stiffness³. To what extent fiber orientation and density have also an influence on the stiffness of the orders of magnitude softer human brain tissue⁴ is yet unclear. We therefore assessed the mechanical stiffness (by determining the shear modulus) of dissected cubic brain specimens via triaxial biomechanical testing and related the findings to tissue microstructural measures obtained from magnetization transfer and diffusion MRI.

Methods

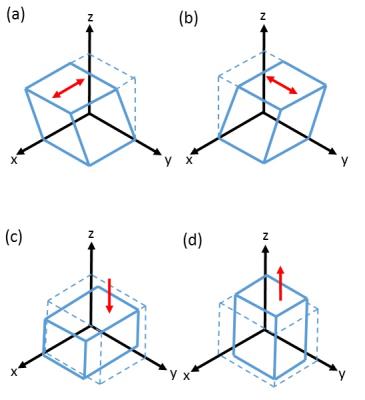
Brain tissue from 6 deceased subjects (mean age 61 ± 2 years, female/male = 2/4) was included in this study. Immediately after autopsy, post-mortem MRI was performed at room temperature at 3T (Siemens Magnetom PRISMA), including a T₁-weighted turbo inversion recovery (TIR) sequence (TR = 5390 ms, TE = 10 ms, TI = 500 ms), a 2D rf-spoiled gradient echo (GRE) sequence (TE = 1050 ms, TE = 4.27, 10.4, 15.88, 21.36, 26.84, 32.32 ms, flip angle = 15°) and a MT-weighted sequence, identical with the GRE sequence parameters, but with an additional off-resonant saturation RF pulse (offset frequency = 1.2 kHz, duration = 10 ms, flip angle = 500°). All these sequences were performed with an in-plane resolution of 1x1 mm² and a slice thickness of 2 mm. Diffusion weighted images (DWI) were acquired using a readout-segmented EPI sequence with 1x1x5 mm³ resolution (TR = 3100 ms, TE = 55 ms, b = 1500 s/mm² applied in 12 directions, 2 averages and GRAPPA = 3). After MRI, the brain was cut in approximately 10 mm-thick coronal slices and tissue cubes with approximately 5x5x5 mm³ were dissected from the corpus callosum, basal ganglia, white matter and cortex and then immediately underwent biomechanical testing³. To determine the mechanical properties under multiple loading modes, the specimens were mounted onto the triaxial testing device (shear in two orthogonal directions, compression and tension) as shown in Figure 1. For each sample tested, the shear modulus µ was determined as a measure for tissue stiffness by calibrating the modified one-term Ogden strain energy function with the response of all conducted loading modes simultaneously⁵. All tests were performed at room temperature and with quasi-static loading conditions at a speed of v = 2 mm/min. The directional dependency of the shear moduli was assessed in samples from the corpus callosum, where specimens were loaded along and perpendicular to the main fiber direction. Mean magnetization transfer ratio (MTR) and fractional anisotropy (FA) were determined for each region dissected for triaxial testing and then correlated with the corresponding shear modulus.

Results

The shear modulus was biomechanically assessed in a total of 42 specimens (14 corpus callosum, 8 basal ganglia, 12 white matter and 8 cortex). The corpus callosum showed the lowest shear moduli (µ = 0.35 ± 0.13 kPa), whereas the shear moduli of the basal ganglia (µ = 0.66 ± 0.22 kPa) were slightly lower than of white matter (µ = 0.71 ± 0.22 kPa). The highest shear moduli were found in the cortex (µ = 1.37 ± 0.34 kPa). No directional dependency of the shear moduli with respect to the corpus callosum fiber orientation was observed. However, the shear modulus was negatively correlated with MTR (r = 0.68, p < 0.001) and FA (r = 0.77, p < 0.001).

Discussion and Conclusion

Our study revealed strong inverse correlations between the shear modulus and MTR and FA. In structures with highly oriented fiber bundles such as the corpus callosum we could not observe directional dependency of the shear moduli. This is in contrast to the situation in the heart or in muscles, where collagen and muscle fibers are mechanically supporting the tissue³. Therefore, we conclude that neuronal fibers are not supporting the tissue matrix from a mechanical point of view. The negative correlation of MTR as biomarker for myelination suggests that the high lipid content of myelinated fibers reduces the mechanical stiffness of brain tissue.

Acknowledgements

No acknowledgement found.