4721
Spectral Diffusion IVIM Analysis of Enlarged Perivascular Spaces in Cerebral Small Vessel Disease1Radiology and Nuclear Medicine, Maastricht University Medical Centre, Maastricht, Netherlands, 2Neurology, Maastricht University Medical Centre, Maastricht, Netherlands
Synopsis
The conventional IVIM model assumes a two-compartment model; this might not apply for regions with enlarged perivascular spaces (PVS) in cerebral small vessel disease (cSVD). Regularized non-negative least squared was used to deconvolve the IVIM signal in multiple diffusion components. Sixty-three cSVD patients and thirty-five controls received IVIM imaging and visual scoring of enlarged PVS. An additional component to the assumed parenchymal and perfusion components was revealed. We show that the fraction of this component is related to the amount of scored enlarged PVS. Quantifying PVS is a time-consuming process and this method might aid the development of automatic quantification.
Introduction
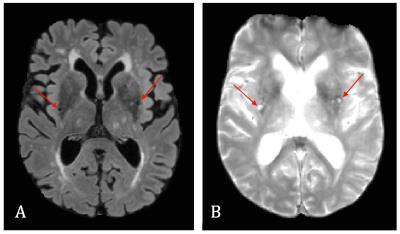
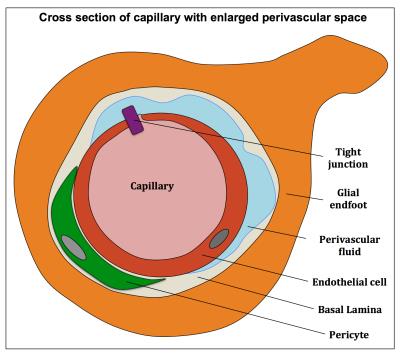
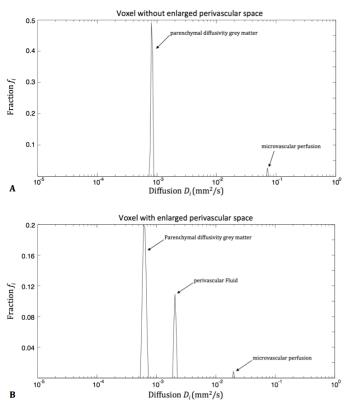
Cerebral small vessel disease (cSVD) is an age-related disease associated with degeneration of both the microvasculature and parenchyma and induces enlarged perivascular spaces (PVS)1, which is one of the radiological markers of cSVD (Fig. 1A-B). Intravoxel Incoherent Motion Imaging (IVIM) can determine the properties of both microvascular and parenchymal structures and can therefore be valuable for this disease. However, whereas the conventional IVIM model assumes a two-compartment model2, this might not apply for certain pathological brain regions in cSVD. For example, in regions with enlarged perivascular spaces (PVS) (Fig. 2), water diffusion in the perivascular fluid (PVF) might strongly contribute to the MRI signal, in addition to parenchymal diffusion and microvascular perfusion-driven pseudo-diffusion. Therefore, a method without assumptions on the number of compartments is required. Previously, a regularized non-negative linear least-squared (NNLS) algorithm was introduced to deconvolve the IVIM signal into multiple components.3,4 We explored this method in cSVD and observed that whereas two diffusion components could be distinguished in the spectrum from a voxel with no enlarged PVS (Fig. 3A), a third component could be seen in the spectrum with enlarged PVS (Fig. 3B). Therefore we aimed to explore the merit of the regularized NNLS algorithm in cSVD, especially in brain tissue with enlarged PVS.Methods
Study population Participants (n=98), consisting of patients with cSVD (n=63, 69.6±11.0y) and controls (n=35, 68.1±11.9y) were scored on enlarged PVS in the basal ganglia by two neurologists. Participants were divided into three groups: those who had low (n=56), moderate (n=22) or high (n=20) prevalence of enlarged PVS.
Data acquisition IVIM imaging was performed for all participants on a 3T MR scanner (Philips Achieva TX). A Stesjkal-Tanner diffusion weighted (DW) spin echo single shot echo planar imaging (EPI) pulse sequence was applied (TR/TE = 6800/84 ms, FOV: 221x269 mm2, 58 slices, 2.4 mm voxel size) using 15 b-values (0, 5, 7, 10, 15, 20, 30, 40, 50, 60, 100, 200, 400, 700, 1000 s/mm2, in the anterior-posterior direction, scan time 5:13 min). To minimize contamination of CSF, an inversion recovery pre-pulse (TI = 2230 ms) was implemented prior to the DW sequence.5
Data analysis The IVIM signal was analyzed per voxel using the regularized NNLS algorithm.6 Here the signal was assumed to be composed of multiple exponential basis functions according to:
$$S_{b}= S_0\cdot\sum_{i=1}^Mf_ie^{-bD_i}$$
where Sb is the signal as a function of the b-value, S0 the signal at b=0 s/mm2, M the number of basis functions, Di the i-th diffusion coefficient (where Di>0), and fi the individual fraction of the corresponding Di. For the algorithm, 250 log-spaced D-values between 0.01–1000·10-3 mm2/s were used. This analysis provides a diffusion spectrum as a function of the corresponding fraction fi (Fig. 3). We defined the D of parenchymal diffusivity to be Di<1.5·10-3 mm2/s, of PVF to be between 1.5≤Di< 4.0·10-3 mm2/s and of microvascular perfusion Di≥4.0·10-3 mm2/s (Fig. 3B). The fraction of perivascular fluid PVF (fPVF), was quantified by taking the sum of the fractions between 1.5≤Di<4.0·10-3 mm2/s. Note that it is expected that these Di values have no or a small fraction in a voxel with low prevalence of enlarged PVS (Fig. 3A), but do have fractions for a voxel with high prevalence of enlarged PVS (Fig. 3B). Mean fPVF was calculated over all voxels in the putamen, a deep grey matter structure, which is part of the basal ganglia and where enlarged PVS can be often found. Mean fPVF were compared between the three groups using a Student's t-test.
Results
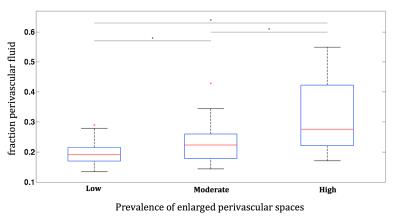
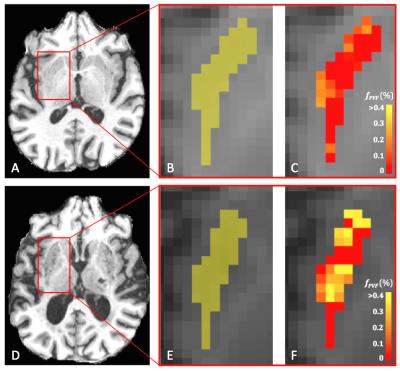
Figure 4 shows boxplots of the mean fPVF in the putamen for all groups. Participants with a high prevalence of enlarged PVS had higher mean fPVF (mean±SD: 0.32±0.11) than those with low (0.19±0.04) or moderate prevalence (0.23±0.07) (p<0.01). Moreover, those with moderate prevalence of enlarged PVS had a higher mean fPVF than those with low prevalence (p=0.03). In Figure 5A-C and 5D-F, T1 weighted images next to a map with fPVF for the putamen with low and high prevalence of enlarged PVS, respectively, are shown.Discussion and conclusion
Employing regularized NNLS, an additional component to the assumed parenchymal and perfusion compartments of the IVIM model was revealed. We show that the fraction of this component is related to the amount of visually scored enlarged PVS. Since this extra component has a higher D than the parenchymal diffusivity (D ≈ 0.7·10-3 mm2/s), when not accounted for, it can contribute to an artificially high perfusion fraction f in the conventional IVIM analysis (e.g. two-step approach). Quantifying PVS is a time-consuming process, and this method might aid the development of automatic quantification.Acknowledgements
No acknowledgement found.References
1. Wardlaw JM, Smith EE, Biessels GJ, et al. Neuroimaging standards for research into small vessel disease and its contribution to ageing and neurodegeneration. Lancet Neurol. 2013;12(8):822–838.
2. Le Bihan D, Breton E, Lallemand D. Separation of Diffusion and Perfusion in Intravoxel Incoherent Motion MR imaging. Radiology. 1988;(168):497–505.
3. Keil VC, Mädler B, Schild HH, et al. Evaluating a Semi-continuous Multi-compartmental Intra-Voxel Incoherent Motion (IVIM) Model in the Brain: How Does the Method Influence the Results in IVIM? Proc. Intl. Soc. Mag. Reson. Med. 23. 2015; 0348.
4. Mädler B and Coenen VA. Performance Evaluation of Various Numerical Algorithms for a Multi-Compartmental IVIM-Model. Proc. Intl. Soc. Mag. Reson. Med. 21. 2013; 3193.
5. Hales PW, Clark C. Combined arterial spin labeling and diffusion-weighted imaging for noninvasive estimation of capillary volume fraction and permeability-surface product in the human brain. J. Cereb. Blood Flow Metab. 2012;(February 2012):67–75.
6. Bjarnason TA, Mitchell JR. AnalyzeNNLS: Magnetic resonance multiexponential decay image analysis. J. Magn. Reson. 2010;206(2):200–204.
Figures