4687
Strategies for Building a Morphologically Faithful Average Brain Template from Population Diffusion MRI Data1Quantitative Medical Imaging Section, NIBIB/NIH, Bethesda, MD, United States, 2SQUITS/NICHD/NIH, Bethesda, MD, United States, 3Henry Jackson Foundation, Bethesda, MD, United States
Synopsis
The availability of anatomically accurate MRI atlases, which can be used as target templates for registration, is essential for quantitative analysis of MRI data. Ideally the computed atlas should be representative of the average features of the population at each voxel location. In this work, we investigate the ability of the most common atlasing approach (i.e. iterative registration followed by averaging) of assuring morphological accuracy. We also evaluate whether constraining the individual deformation fields with deformation-based information helps achieving this goal. We perform our atlas creation tests from full DTI data, using a novel diffusion tensor based diffeomorphic registration technique. We conclude that current atlasing techniques lead to templates that do not faithfully represent the average morphology of the population but that by applying appropriate constraints significant improvements toward this goal can be achieved.
Introduction
The availability of anatomically accurate MRI atlases that can be used as target templates for registration, is essential for quantitative analysis of MRI data. Ideally the computed atlas should be representative of the average features of the population at each voxel location. In this work, we investigate, the ability of assuring morphological accuracy of common template creation strategies, which rely on diffeomorphic registration of individual subjects [1,2]. These diffeomorphic methods generally consist of a linear (affine) component plus a higher order component of the deformation. While it is generally accepted that constraints need to be imposed in order to guarantee that the resulting template is representative of the average features of the population, current approaches apply constraints only to the affine component of the registration. In this work we analyze if constraints for the higher order components are necessary either on the displacement fields [3] or the underlying velocity fields [4]. The goal of this work is to investigate the effects and necessity of such constraints on diffusion MRI based population atlases. Although MRI atlases have been typically created from structural MRIs or scalar DTI maps, without loss of generality, we perform our tests using a novel diffusion tensor based diffeomorphic technique, which employs full DTI data to drive the registration [5].Materials
DWIs were collected on 15 volunteers on a 3T Philips scanner with a single-shot spin-echo EPI sequence (resolution=2mm isotropic, matrix size=112x112, 80 slices, TR/TE=10463/83.7ms). Acquisitions consisted of 6 volumes with b=0 s/mm2, 40 volumes with b=1100 s/mm2, repeated four times with phase encoding directions AP, PA, RL, LR. DWIs were corrected for motion, eddy-currents distortions [6] and morphological alignment to a structural image was achieved by using all phase encoding direction data for EPI distortion correction [7]. Fat suppressed T2-weighted images were also acquired at 1x1x2 mm resolution.Methods
For diffeomorphic tensor registration, we used the recently developed DR-TAMAS [5] tool, which has been shown to produce accurate alignment across all brain regions. For atlas creation we followed the principles proposed by Joshi et al. [1] for the unconstrained case, and followed the strategy in [4] to impose morphometry constraints for the higher order deformation, with a modification to include the necessary changes in the deformation fields of each individual.
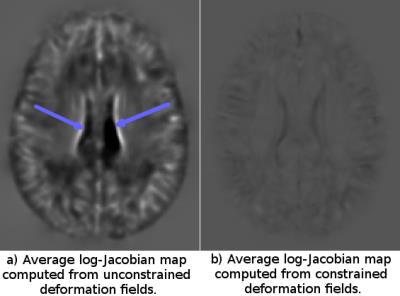
Shape Constraints on Deformation Fields: A reasonable requirement in atlas creation is that each structure in the computed template should be the average of the original individual structures in terms of size, shape and appearance. This implies that at each voxel location the volume of the structure depicted should be equal to the sum of the volumes of the individuals composing the population. Therefore, in tensor-based morphometry analysis [8] the sum of the individual log of determinant of the Jacobian of the deformation fields should be zero:$$$\sum_{i=1}^Nlog\left( det\left( \frac{\partial \phi_i(x)}{\partial \mathbf{x}}\right)\right)=0$$$ $$$\forall x$$$. In our constrained framework, this is achieved as follows: Let $$$\phi_i(x)$$$ be the deformation that maps the voxel $$$x$$$ in the template to its corresponding location in image i. The average backwards deformation field is computed as: $$$\overline{\phi}(x)= \frac{1}{N} \sum_{i=1}^N \phi_i(x)$$$. Combining the inverse of this average displacement field with each of the original fields as, $$$\phi_i'(x)= \phi_i \circ \overline{\phi}^{-1}(x)$$$ and re-computing the template at each iteration satisfies all the desired properties in a simplistic way. The average log-Jacobian (logJ) maps were computed for each method and the presence of structures in these maps were assessed.
Results
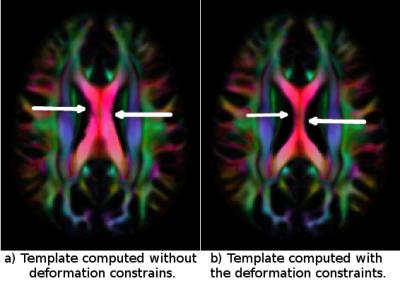
Figure 1 displays the average of the log Jacobian maps for both approaches. For the template constructed without any constraints logJ map shows a number of regions with positive or negative values. For example, strongly negative log-Jacobian values can be seen in the Corpus Callosum (CC) region. This indicates that the size of CC in the computed template (Fig2A) is not a faithful representation of the average size of the CC of the individual subjects because it consistently requires to be compressed to match them. On the other hand, in the constrained case, the LogJ values in the CC are almost equal to zero ensuring that the size of the CC in the template (Fig2 B) is anatomically representative of the population.Conclusions
Regularizing the shapes of the brain structures in an atlas creation framework using the deformation fields, mapping the original subjects to template has a very significant impact on the quality of the final template. This effect is even more prominent if the sizes of different brain structures or the deformation fields themselves are considered in an analysis framework and can lead to inaccurate/incorrect conclusions.Acknowledgements
Support for this work included funding from the Congressionally Directed Medical Research Programs (CDMRP).References
1. Joshi S., Davis B., Jomier M., Gerig G. , Unbiased diffeomorphic atlas construction for computational anatomy, Neuroimage. 2004;23 Suppl 1:S151-60.
2. Zhang, H., Avants, B.B, Yushkevich, P.A., Woo, J.H., Wang, S., McCluskey, L.H., Elman, L.B., Melhem, E.R., Gee, J.C., High-dimensional spatial normalization of diffusion tensor images improves the detection of white matter differences in amyotrophic lateral sclerosis, IEEE Transactions on Medical Imaging, 26(11):1585-1597, November 2007.
3. K. K. Bhatia and J. V. Hajnal and B. K. Puri and A. D. Edwards and D. Rueckert, Consistent groupwise non-rigid registration for atlas construction, Proceedings of the IEEE Symposium on Biomedical Imaging (ISBI), 2004, pp. 908—911.
4. Avants BB, Yushkevich P, Pluta J, Minkoff D, Korczykowski M, Detre J, Gee JC., The optimal template effect in hippocampus studies of diseased populations., Neuroimage. 2010 Feb 1;49(3):2457-66.
5. Irfanoglu MO, Nayak A, Jenkins J, Hutchinson EB, Sadeghi N, Thomas CP, and Pierpaoli C. 2016. DR-TAMAS: Diffeomorphic Registration for Tensor Accurate Alignment of Anatomical Structures. Neuroimage 132:439–454.
6. C. Pierpaoli, L. Walker, M. O. Irfanoglu, A. Barnett, P. Basser, L-C. Chang, C. Koay, S. Pajevic, G. Rohde, J. Sarlls, and M. Wu. (2010) TORTOISE: an integrated software package for processing of diffusion MRI data. In ISMRM 18th Annual Meeting and Exhibition, Stockholm, Sweden. May 1-7, 2010.
7. Irfanoglu MO, Modi P, Nayak A, Hutchinson EB, Sarlls J, and Pierpaoli C. DR-BUDDI (Diffeomorphic Registration for Blip-Up blip-Down Diffusion Imaging) method for correcting echo planar imaging distortions. NeuroImage 106 (2015) 284–299.
8. Ashburner J1, Friston KJ., Voxel-based morphometry--the methods. Neuroimage. 2000 Jun;11(6 Pt 1):805-21.
Figures