4538
Water exchange in a white matter tissue phantom measured using clinically feasible diffusion exchange spectroscopy (DEXSY) MRI1Quantitative Imaging and Tissue Sciences, National Institutes of Health, Bethesda, MD, United States, 2Center for Neuroscience and Regenerative Medicine, Bethesda, MD, United States
Synopsis
Studying the axons’ membrane permeability at different white matter tracts could clarify the role of aquaporins. Diffusion exchange spectroscopy (DEXSY) is an assumption-free approach to measure water exchange, allowing for any number of exchange processes between any number of compartments. It has never been applied in biological MRI owing to its exceptionally long scan time requirements. Here we present a method to reduce the number of required acquisitions, making DEXSY-MRI clinically feasible for the first time. We apply this method on a nerve tissue phantom, and demonstrate that 14 acquisitions are sufficient to determine the exchange spectrum.
Introduction
During molecular exchange between microenvironments in the brain, water passes across cell membranes, either directly through the lipid bilayers or via channels, such as aquaporins (AQP).1 AQPs represent a diverse family of membrane proteins, with AQP1 and AQP4 being the primary channels expressed in the mammalian brain.2,3 These AQPs ability to facilitate water transport is implicated in pathological conditions such as cancer and brain.4 Most MRI methods for determining membrane transport rates rely on trans-membrane differences in the relaxation times, and often involve the injection of contrast agents (e.g., dynamic contrast-enhanced MRI5). These methods all rely on biophysical models that assume there are only two microenvironments that exchange. A recent diffusion-based method to map water exchange makes the same assumption of only two exchanging compartments with slow and fast diffusion rates.6 Avoiding such assumptions, we suggest using an assumption-free approach to measure exchange, allowing for any number of exchange processes between any number of compartments. Diffusion exchange spectroscopy (DEXSY)7 is a 2D double pulsed-field gradient experiment that provides this functionality. As powerful as it is, it has never been applied in biological MRI owing to its exceptionally long scan time requirements. Here we present a method to vastly reduce the number of required acquisitions, making DEXSY-MRI clinically feasible for the first time.Methods
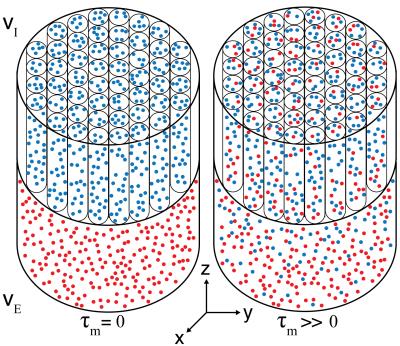
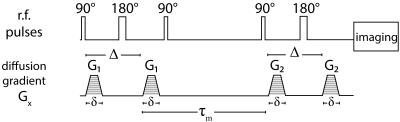
A white matter phantom was comprised of a water-filled glass capillary array with a nominal inner diameter of 5$$$\mu$$$m, and an adjacent layer of freely diffusing water, mimicking intra- and extra-axonal spaces (Fig. 1). Water molecules in the capillaries are free to diffuse along the symmetry axis to the free water pool, and vice versa, resulting in water exchange between restricted and unrestricted compartments. The composite phantom was put in a 15mm NMR tube and scanned using a 7T Bruker vertical wide-bore magnet with an AVANCE III MRI spectrometer. DEXSY-filtered MRI data were acquired by applying the sequence in Fig. 2 followed by a 2D spin echo MRI sequence. Diffusion gradients, G1 and G2, are applied in the same direction ($$$x$$$, see Fig. 1), and their amplitudes are varied independently with 45 linear steps (resulting in $$$N=45\times45=2025$$$ acquisitions) in the range of 0-1346mT/m, leading to $$$b=\gamma^2\delta^2G^2(\Delta-\delta/3)$$$ in the range of 0-18180s/mm2, and $$$\tau_m$$$=15,200,300ms. The resulting signal as a function of the applied b-values is given by
$$M(b_{1},b_{2})=\sum_{n=1}^{N_{D_{1}}}\sum_{m=1}^{N_{D_2}}{{\mathbf{F}(D_{1,n},D_{2,m})\,\exp(-b_1D_1-b_2D_2)}}$$
where $$$\mathbf{F}(D_{1},D_{2})$$$ is the joint probability of the contribution to the signal from the initial diffusion coefficient, D1, and the final diffusion coefficient, D2. In this work we apply a recently proposed method8 to stabilize the estimates of $$$\mathbf{F}(D_1,D_2)$$$ in Eq. 1, while reducing the number of acquisitions and improving accuracy, by constraining the solution according to the following relation:
$$\sum_{n=1}^{N_{D_1}}{\mathbf{F}(D_1,D_{2,n})}=\sum_{n=1}^{N_{D_2}}{\mathbf{F}(D_{1,n},D_2)}=F(D).$$
The 1D distribution, $$$F(D)$$$, can be separately estimated from a 1D experiment, which requires an order of magnitude less data than a conventional 2D acquisition.
Results and Discussion
The
volume fraction of water that remains in the capillaries/free-water
compartment after the mixing time is $$$f_{I}/f_{E}$$$ and the volume that
diffused from one space to the other and vice versa is $$$f_{IE}/f_{EI}$$$.
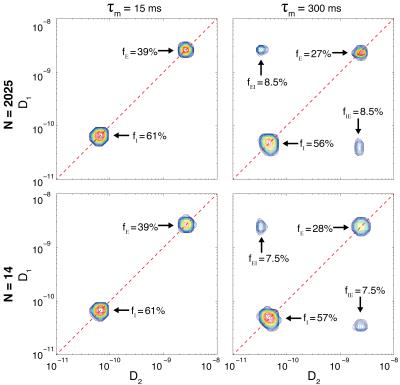
Processing the 2D data using Eqs. 1&2 results in the
$$$\mathbf{F}(D_1,D_2)$$$ spectra presented in Fig. 3. The distributions on the
top row are obtained by using the entire dataset, and the ones on the bottom are
obtained by using only 0.07% of the data. The suggested method allows for a
vast reduction of required data, while yielding highly accurate results. The
peaks on the diagonal of the distributions are $$$f_{I}$$$ and
$$$f_{E}$$$, and the off-diagonal peaks are $$$f_{IE}$$$ and $$$f_{EI}$$$,
which should be equal in an equilibrated system. As
expected, $$$f_{I}$$$/$$$f_{E}$$$ decrease
and $$$f_{IE}$$$/$$$f_{EI}$$$ increase as a function of $$$\tau_m$$$. When
complete exchange has occurred the off-diagonal peaks should have an intensity
of 25%, a value which reflects the equilibrium probability distribution of
water between the restricted and free states. Assuming an exponential process,
we may estimate the exchange rate, $$$k_{exc}\sim1.1$$$1/s, and the exchange
time, $$$\tau_{exc}\sim0.9$$$s. We showed that 14 acquisitions are sufficient to
accurately determine the diffusion exchange spectrum, which is $$$\sim150$$$
times less than previously thought to be needed. Combined with an EPI readout, this approach makes DEXSY MRI a clinically feasible imaging
technique to measure the water exchange rate.Conclusion
AQPs' function in the healthy brain is only partially understood, therefore studying the water exchange rate from and to axons at different white matter tracts could clarify their role. This method is not limited to any number of predetermined compartments and exchange processes, thus it can also be used to image water exchange and dynamics in gray matter.Acknowledgements
No acknowledgement found.References
1. Agre P, King LS, Yasui M, Guggino WB, Ottersen OP, Fujiyoshi Y, Engel A, Nielsen S. Aquaporin water channels - from atomic structure to clinical medicine. J Physiol 2002; 542: 3–16.
2. Nielsen S, Nagelhus EA, Amiry-Moghaddam M, Bourque C, Agre P, Ottersen OP. Specialized membrane domains for water transport in glial cells: high-resolution immunogold cytochemistry of aquaporin-4 in rat brain. J Neurosci. 1997;17(1):171-80.
3. Oshio K, Watanabe H, Yan D, Verkman AS, Manley GT. Impaired pain sensation in mice lacking Aquaporin-1 water channels. Biochem Biophys Res Commun. 2006;341:1022–1028.
4. Tait MJ, Saadoun S, Bell BA, Papadopoulos MC. Water movements in the brain: role of aquaporins. Trends Neurosci 2008; 31: 37–43.
5. Tofts PS, Kermode AG. Measurement of the blood-brain barrier permeability and leakage space using dynamic MR imaging. 1. Fundamental concepts. Magn Reson Med. 1991;17(2):357-67.
6. Nilsson M, Lätt J, van Westen D, Brockstedt S, Lasic S, Ståhlberg F, Topgaard D. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magn Reson Med. 2013;69(6):1573-81.
7. Callaghan PT, Furo I. Diffusion–diffusion correlation and exchange as a signature for local order and dynamics. J Chem Phys 2004; 120: 4032–4038.
8. Benjamini D, Basser PJ, Joint radius-length distribution as a measure of anisotropic pore eccentricity: an experimental and analytical framework. J Chem Phys. 2014;141:214202.
Figures