Purpose

The rotating RF coil (RRFC) is capable of imaging an entire volume with a single coil and multiple receive sensitivities since the position of the coil changes with time ^1-3. To reconstruct an image from a Cartesian k-space, sensitivity mapping and iterative algorithms are required to eliminate motion artifacts caused by coil rotation ². Our previously developed scheme partially addressed these issues by exploiting radial sampling ³. However, only the central k-space with adequate oversampling is most efficient for sensitivity reformation during regridding ³. Cartesian sampling is the most used sampling scheme and offers robust performance with accurate gradient trajectories and simple reconstruction by inverse fast Fourier transformation (IFFT). Here we propose an imaging method with Cartesian trajectories for the RRFC without mapping sensitivity profiles experimentally or iterative algorithms. Simulation is used to analyse and validate this method.

Methods

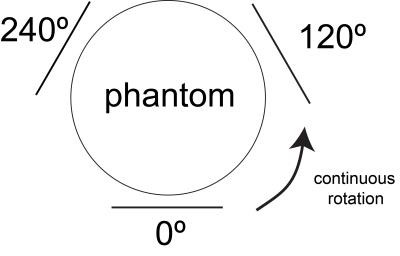
The RRFC prototype for a 9.4T animal system contains a 26 mm (longitudinal) and 60° open-angle loop coil, wrapped around a 40 mm diameter rotary coil former. The electromagnetic simulation software FEKO (Hyperworks, USA) and Matlab (Massachusetts, USA) were used to acquire rotation-dependent sensitivities, which were then used to simulate k-space data. As shown in Eq.1, each k-space sample is encoded with a dynamic sensitivity S(r,α) due to coil rotation. After applying IFFT on such k-space data, an image contaminated with motion artifact will be produced. As shown in previous work ³ and in Fig.1, three sensitivity profiles with 120° angular increment will generate a uniform sensitivity with the current coil geometry. Thus it is possible to adjust the angular speed, so that combined successive Cartesian k-spaces are associated with uniform sensitivity for artifact-free image recovery. The mathematical expression is shown in Eq.2. Each k-space sample in the final image is an average from three k-space samples with different sensitivities of corresponding phase-encoding lines. The uniformity of the averaged sensitivity $$$\overline{S}$$$ is critical to reconstruction quality, because samples in the combined k-space will have the same sensitivity once $$$\overline{S}$$$ is uniform, thus IFFT is applicable for fast image reconstruction. As shown in Fig.1, with a desired angular increment (θ) of 120°, each phase encoding (PE) line is encoded with sensitivities in 120° separation. The image size (IS) is carefully chosen to satisfy mod(IS,360°/θ)≠0 so that each k-space will have a different initial start position. Otherwise, sensitivity profiles for the corresponding PE lines in three k-spaces will have the same sensitivity and averaging of all k-spaces will not generate a uniform sensitivity.

Results

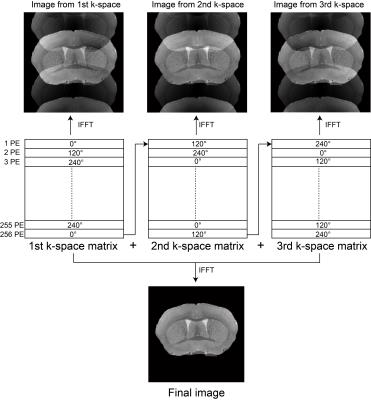
In Fig.2, samples in three k-space matrices were encoded with different sensitivity profiles, thus images recovered from individual k-space matrix exhibited motion artifacts. However, after combining three k-space matrices, each k-space sample had the same uniform sensitivity; therefore, applying IFFT generated an artifact-free final image. With sub-optimal choice of θ and IS (θ = 90° and IS = 256), sensitivity profiles at the corresponding PE lines of three k-spaces were the same (mod(256,360°/90°)=0). Therefore, each PE line in the combined k-space had different sensitivity weightings, causing motion artifacts (Fig.3a). With the golden angle (θ = 111.246° to assure the sampling locations are uniformly distributed around the subject), sensitivity profiles at corresponding PE lines of three k-spaces were different; however, combined sensitivity profiles of three PE lines could not generate a uniform sensitivity. Therefore, the samples in the combined k-space had different sensitivity encodings, leading to artifacts in the recovered image (Fig.3(c)). The maximum error in the image recovered with optimal 120° angular increment is 78% and 75% smaller than that of the images recovered with 90° and 111.246° angular increment.

Discussion

The speed variation of RRFC was about 5% using a two-stage air regulator for the pneumatic drive. With 100ms TR and 200rpm rotation speed (lowest speed for the optimal 120° θ), coil position variation was only about 0.08° during a 1.28 ms acquisition time (time acquiring a PE line). Therefore, after averaging dynamic sensitivities in three k-spaces, the sensitivity profiles of each phase-encoding line were still uniform regardless of the minor speed variation. The current RRFC prototype has only one coil element, additional coil elements can increase sensitivity coverage and reduce the number of k-spaces needed for image recovery.

Conclusion

In this proof-of-concept work, the proposed method can dramatically reduce motion artifacts through combining multiple k-space samples with carefully chosen rotation speed and imaging parameters. The consequent optimal 120° angular increment guaranteed the uniform sensitivity generation in the final combined k-space; therefore, the direct IFFT could be applied for fast image reconstruction without using iterative algorithms and sensitivity maps.

Acknowledgements

This work was supported by the Australian Research Council Linkage Projects ( LP120200375).