4424

Fast 3D Design of High-Permittivity Pads for Dielectric Shimming using Model Order Reduction and Nonlinear Optimization

Jeroen van Gemert¹, Wyger Brink², Andrew Webb², and Rob Remis¹

¹Circuits and Systems, Delft University of Technology, Delft, Netherlands, ²Radiology, Leiden University Medical Center, Leiden, Netherlands

Synopsis

High-permittivity pads can be used to improve B₁⁺ homogeneity and intensity in neuroimaging and body applications. Normally, finding the “optimal” pad for a specific region of interest involves evaluating many different pad designs using electromagnetic simulations, which is a very time-consuming approach taking hours to days of computation time. We propose a nonlinear optimization method based on model order reduction that allows us to design high-permittivity pads in less than 30 seconds.

Purpose

Analyzing high-permittivity pads to improve B₁⁺ homogeneity and intensity is normally accomplished by using full-wave solvers.¹ The “optimal” design is found by evaluating a large number of pad realizations, typically, covering only a subset of the design parameters such as the permittivity, dimension, and location of the pad.^2,3 This optimization process is computationally intensive, taking hours or even days to complete. We have shown previously that the process of evaluating such pad realizations can be accelerated by means of domain decomposition.⁴ This decomposition allows us to generate a pad-independent library for a pad design domain into which the dielectric pad can subsequently be positioned. In the current work we present further speed improvements by compressing this library significantly, such that the optimal pad can be found within 30 seconds using nonlinear optimization techniques.

Methods

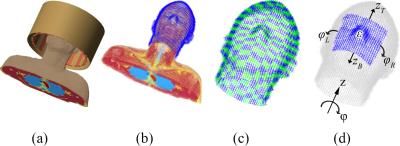
A spatial resolution of 5 mm³ is used for modeling the human head and corresponding RF fields for a 7T (298 MHz) neuroimaging application. The virtual family member “Duke” is used as body model⁵ combined with a 16-rung high-pass birdcage coil as shown in Figure 1(a). For the domain decomposition we consider a 1 cm thick pad design domain surrounding the head, as shown in Figure 1(b). Computations are performed with Remcom XFdtd (v.7.5.0.3) and Matlab (R2014b) on a Windows 64-bit machine (Intel Xeon CPU X5660@2.80 GHz, 48 GB memory, two NVIDIA Tesla K40c GPU’s).

Since we do not need a 5 mm³ resolution for designing dielectric pads, we artificially decrease the resolution by subdividing the pad design domain into 400 subdomains of approximately 2×2×1 cm³ as is shown in Figure 1(c). We then parameterize the design domain to model a rectangular pad with a single permittivity by using a superposition of Heaviside step functions. In such a way, we formulate the design problem as an optimization of five variables only, as illustrated in Figure 1(d).

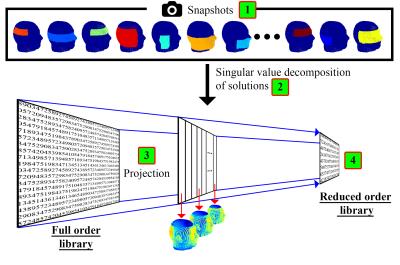
Within the range of pads that can be generated using this parameterization and subdomains, we can now compress the size of the original full order library by dispensing with information that does not contribute to the associated range of B₁⁺ solutions. This compression is obtained by evaluating a series of pad realizations or “snapshots” where randomized values are assigned to our five design parameters. The resulting electric current density in the pad design domain is stored for each realization. Hereafter, the 500 most significant contributions are extracted by using a singular value decomposition, which forms a projection matrix.⁶ Finally, we project the library using this projection matrix on a new reduced order library giving us a Reduced Order Model (ROM). This process is illustrated in Figure 2.

For the optimization we define a cost function that is to be minimized as

$$C(\boldsymbol{p})=\frac{\lVert \boldsymbol{b}_1^+(\boldsymbol{p})- \boldsymbol{b}_1^{+\text{;desired}} \rVert^2_2}{\lVert \boldsymbol{b}_1^{+\text{;desired}} \rVert^2_2}$$

where $$$\boldsymbol{b}_1^+(\boldsymbol{p})$$$ is the B₁⁺ field computed by the ROM and $$$\boldsymbol{b}_1^{+\text{;desired}}$$$ is the desired B₁⁺ field intensity which is set to 1.2 µT. Finally, vector $$$p$$$ contains the parameters of the pad. The nonlinear optimization problem is solved using a Gauss-Newton algorithm combined with backtracking line search to determine the stepsize.

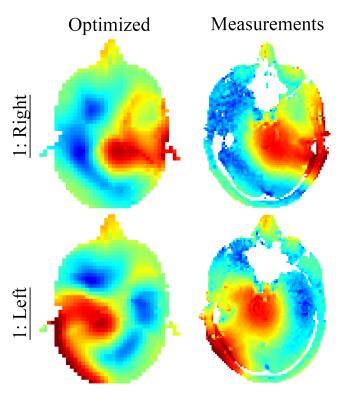
The optimized pads have been implemented using a stabilized suspension of barium and calcium titanate⁷ such that the B₁⁺ maps can be compared with measured data obtained in vivo using a DREAM B₁⁺ mapping sequence.⁸

Results

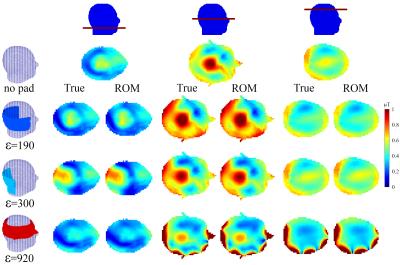
The model order reduction procedure compresses the library for the pad design domain, from 29 GB to 1 GB. Evaluating the B₁⁺ field using the full order model completes in about 90 seconds when using GMRES (tolerance=10^-4), whereas the ROM completes in 0.35 seconds when using a direct solver (≈250x speedup). A comparison of the B₁⁺ fields for different dielectric pads obtained using the full order model and ROM is shown in Figure 3, where the global error in B₁⁺ magnitude is around 5%.

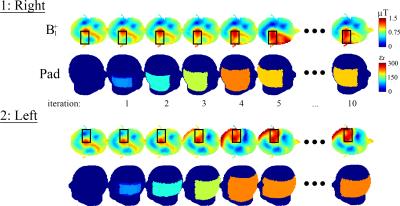
The evolution of the optimization method for two scenarios is shown in Figure 4, where the region of interests are indicated by black squares. Within 10 iterations and 30 seconds the method converges to a dielectric pad with a relative permittivity of 200 and 220, respectively, with corresponding dimensions of 13×16×1 cm³ and 13×22×1 cm³. The in vivo results are in good agreement as shown in Figure 5.

Discussion and conclusion

Practical dielectric pads can be designed in 3D within 30 seconds using the parameterized ROM and the optimization scheme. With the ROM, the B₁⁺ field in the entire head can be obtained in 0.35 seconds for any dielectric pad. This approach can facilitate efficient 3D design of high-permittivity pads for dielectric shimming in high-field MRI.

Acknowledgements

This research was funded by the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO), STW Project #13375.

References

[1] Yang QX, Wang J, Collins CM, et al, Reducing SAR and enhancing cerebral signal-to-noise ratio with high permittivity padding at 3 T. Magn Reson Med. 2011;65(2):358-362.

[2] Brink WM, Webb AG. High permittivity pads reduce specific absorption rate, improve B1 homogeneity, and increase contrast-to-noise ratio for functional cardiac MRI at 3 T. Magn Reson Med. 2014;71(4):1632-1640.

[3] Teeuwisse WM, Brink WM, Haines KN, Webb AG. Simulations of high permittivity materials for 7 T neuroimaging and evaluation of a new barium titanate-based dielectric. Magn Reson Med. 2012;67(4):912-918.

[4] Gemert JHF, Brink WM, Webb AG, Remis RF. An Efficient Methodology for the Analysis of Dielectric Shimming Materials in Magnetic Resonance Imaging. IEEE Trans Med Imag. 2016. DOI 10.1109/TMI.2016.2624507.

[5] Christ A. The Virtual Family development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys. Med. Biol. 2010;55(2):23-28.

[6] Quarteroni A, Gianluigi R. Reduced Order Methods for Modeling and Computational Reduction. Vol. 9. Ch. 2. Springer, 2014.

[7] O’Reilly TPA, Webb AG, Brink WM. Practical improvements in the design of high permittivity pads for dielectric shimming in neuroimaging at 7T. J Magn Reson. 2016;270:108-114.

[8] Nehrke K, Börnert P. DREAM-A Novel Approach for Robust, Ultrafast, Multislice B1 Mapping. Magn Reson Med 2012;68:1517–1526.

Figures

Figure 1: Model description. The head model Duke is positioned in a 7T quadrature birdcage coil (a). The pad design domain is defined to be 1 cm thick surrounding the head (b). The design domain is divided into 400 subdomains (c). The model is parameterized such that the position, dimensions, and permittivity of a rectangular pad can easily be defined (d).

Figure 2: Overview of the model order reduction procedure. First, a series of snapshots is created by simulating a variety of high-permittivity pads (1). The solutions are stored in a snapshot matrix, after which a singular value decomposition is performed to extract the 500 most significant contributions. These contributions form the projection matrix (2). Three significant components of this projection matrix are shown at the bottom. The full order library is then projected (3) using the projection matrix to obtain our desired reduced order library (4).

Figure 3: A comparison between the “true” B₁⁺ field calculated using the full order and the reduced order model. The top row indicates the position of three different slices on which the B₁⁺ fields are evaluated. The left column indicates what kind of pad is used for comparison. The top row with B₁⁺ fields is the result when no pad is used. The remaining plots are the true (left) and the reduced order solution (right).

Figure 4: Overview of optimization results for two scenarios. A region of interest is selected (one in the left hemisphere and one in the right hemisphere), indicated by the black square in the first and third row with B₁⁺ fields for a transverse slice. The second and fourth row show the dielectric pad with corresponding permittivity, where the head is viewed from the right and left hand side, respectively. The optimal dielectric pad is found within 10 iterations, with a total time of 30 seconds. The results are shown for most of the iterations.

Figure 5: In vivo validation of the optimized dielectric pads. The optimized B₁⁺ fields are shown in the left column and in vivo measurements in the right column. In vivo data is acquired using a DREAM B₁⁺ mapping sequence (2.5 mm² resolution, 5 mm slice thickness, STEAM/imaging tip angle = 50°/10°).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

4424