4336
A new method for optimizing performances of gradient coils based on singular value decomposition and genetic algorithm1Institute of Applied Physics, University of Tsukuba, Tsukuba, Japan
Synopsis
Designing gradients coils with arbitrary geometries has been realized by matrix inversion optimization techniques. Use of a truncated singular value decomposition (SVD) is promising because magnetic field accuracies are controlled by choosing the appropriate SVD eigenmodes. However, in the SVD method, the gradient performances, such as inductance and power dissipation, cannot be optimized. Here we proposed a new strategy to optimize a desired coil performance. A key feature is the use of a genetic algorithm to optimize the appropriate combination of SVD eigenmodes. The concept is demonstrated for a biplanar geometry, and would be readily applicable to arbitrary geometries.
INTRODUCTION
Designing gradients coils with arbitrary geometries has attracted much attraction and been realized by matrix inversion optimization techniques combined with discrete representations of current surfaces1. The use of a truncated singular value decomposition (SVD) to solve the matrix inversion problem is promising2,3 because magnetic field accuracies are controlled by choosing the appropriate number of eigenmodes that have major contributions to the magnetic field. However, the selection method of the eigenmodes is empirical, and hence the gradient performances, such as coil inductance and power dissipation, cannot be controlled and optimized. Here we propose a new strategy to optimize a desired coil performance. A key feature is the use of a genetic algorithm (GA) to optimize the appropriate weighted combination of eigenmodes. The concept is demonstrated for a biplanar geometry, and would be readily applicable to arbitrary geometries.DESIGN METHOD
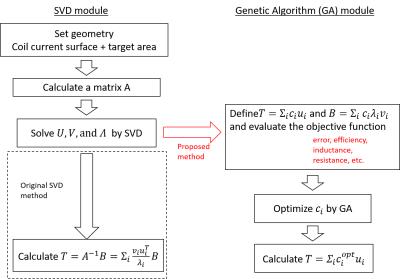
Figure 1 shows a simplified depiction of the design pipeline. For the SVD module, the coil current surface is discretized into a mesh of triangles and the stream function of the current density, or the current potential, at each node $$$i$$$ is defined as $$$T_i$$$. The magnetic field at a point $$$j$$$ in the target area is expressed as $$$B_j = \sum_i^NA_{ij}T_i$$$. Here the matrix $$$A$$$ is calculated using the Bio-Savart law. Then the matrix $$$A$$$ is decomposed using the SVD as $$$A=U \Lambda V^T$$$ where $$$U$$$ and $$$V$$$ are unitary matrices, and $$$\Lambda$$$ is a diagonal matrix containing the singular values $$$\lambda _i , i=1,\cdots ,min(n,m)$$$. Using the columns of $$$U$$$, denoted $$$u_1,\cdots ,u_n$$$, and those of $$$V$$$, denoted $$$v_1,\cdots ,v_m$$$, $$$A=\sum_i^N \lambda _iu_iv_i^T$$$. In the original SVD method, the solution, current potential matrix $$$T$$$, is calculated as $$$T=A^{-1}B=\sum_i^k \frac{v_iu_i^T}{\lambda _i}B$$$. Here $$$k$$$ is the truncation number which is empirically determined depending on the given geometry. Instead in the proposed method, $$$B$$$ and $$$T$$$ are newly formulated as $$B=\sum_i^{k'} c_i\lambda _i u_i,$$ and $$T=\sum_i^{k'} c_iv_i.$$ Then the coefficients $$$\{c_i\}$$$ is optimized by GA to maximize an objective function formulated to quantify the desired coil performance. Here we generalize the objective function as $$f=\frac{\eta^a}{E^bL^cR^d}$$ where $$$\eta$$$ is the coil efficiency, $$$E$$$ is the gradient inhomogeneity, $$$L$$$ is the inductance, and $$$R$$$ is the resistance. The constants $$$a,b,c$$$ and $$$d$$$ are weighing factors to balance these measures. For example, when $$$a=2, b=1, c=1$$$, and $$$d=0$$$, $$$f$$$ corresponds to figure of merit proposed by Turner4.
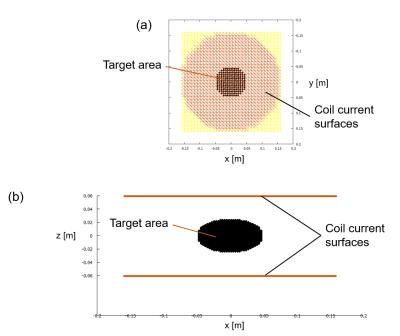
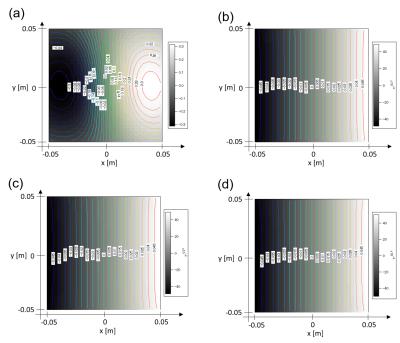
The proposed method was tested to design transverse coils with a biplanar geometry (coil diameter = 320 mm; coil gap = 120 mm). The target region was set to be a 100 mm x 100 mm x 50 mm diameter ellipsoidal volume (Fig. 2). $$$k'$$$was set to 8 for simplicity. We used a real-coded GA algorithm (population size = 50; crossover rate = 75%; mutation rate = 1%) with BLX-$$$\alpha$$$ crossover $$$(\alpha =1)$$$ and an elite selection. We designed coils for different objective functions.
RESULTS AND DISCUSSION
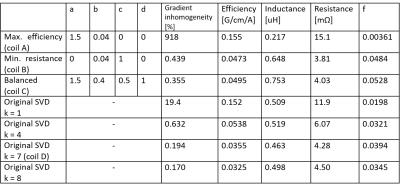
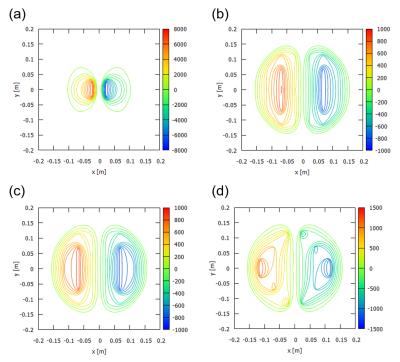
Table 1, Fig. 3, and Fig. 4 summarize the coil performances, coil patterns, and the gradient fields for gradients designed by the proposed method with different objective functions. For comparison, the results obtained with the original SVD method were also shown. For the efficiency-maximized design (coil A), the efficiency was the highest but the gradient inhomogeneity was enormous. For the resistance-minimized design (coil B), the coil pattern was relatively sparse and it is easy to be constructed. Overall, the coil performances were high for the balanced design (coil C). In contrast, the original method gave the less flexible results. As the truncation number increased, the gradient homogeneity increased but the efficiency decreased.CONCLUSION
We proposed a new method for designing gradients with arbitrary geometries. We demonstrated that the combination of the SVD method with GA allows the optimization of the desired performances.Acknowledgements
No acknowledgement found.References
1Poole, M, et al., Concepts in Magnetic Resonance Part B: Magnetic Resonance Engineering 31.3 (2007).
2M. Abe et al., Phys. Plasmas, 10 (2003)
3M. Abe, IEEE Trans. Magn., 49 (2013)
4Turner, R., Journal of Physics E: Scientific Instruments 21.10 (1988).
Figures