Synopsis

The value of ring capacitors in elliptical birdcage coil (EBC) should be varied gradually according to the location of the ring capacitor in order to generate uniform B₁⁺ field distribution. Usually, it is difficult to adjust the value of the ring capacitor precisely by using fixed capacitors, because the value of the fixed capacitor is discretized. To realize the easy fabrication of EBC, we have designed EBC with constant ring-capacitor value at 1.5T. Simulation and experimental results indicated that the designed EBC generated uniform B₁⁺ field distribution and showed the same transmission efficiency as the conventional EBC.

Introduction

Methods

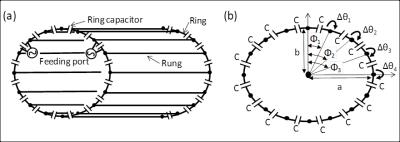
Coil Design: Figure 1 shows the structure of EBC with constant ring-capacitor value. We analyzed the condition of circuit parameters which generated uniform B₁⁺ distribution by the equivalent circuit analysis under the condition that all values of ring capacitors were identical. As a result, we found that EBC with constant ring-capacitor value generated uniform B₁⁺ distribution when the dimensions and circuit parameters satisfied the following equations;

$$\Phi_{m}=\tan^{-1}(\frac{b}{a}\tan(\sum_{k=1}^m\frac{\triangle {\theta}_{k}+\triangle {\theta}_{k+1}}{2}))$$

$$\cos(\triangle\theta_{k+1})=1+\frac{1}{L_{k+1}^l}((L_{k}^r-L_{k-1}^r)+L_{k-1}^l(\cos(\theta_{k-1})-1))$$

$$\sin(\triangle\theta_{k+1})=\frac{L_k^l}{L_{k+1}^l}\sin(\triangle\theta_{k})$$

$$\sum_{k=1}^N(\triangle\theta_{k}+\triangle\theta_{k+1})=2\pi$$

where L^r_k and L^l_k are k-th ring and rung inductances, respectively. Φ_m is angle of m-th rung shown in Fig. 1. N is total number of rungs. Δθ_k is k-th phase difference between adjacent two ring capacitors as shown in Fig. 1. a and b are lengths of major and minor axes in the ring element of EBC, respectively. L^r_k, L^l_k, Φ_m, and Δθ_k were calculated from numerical simulation.³ The width of ring can be calculated from the obtained L^r_k. The width of rung can be calculated from L^l_k and the length of rung (l_r). The ring capacitor value C can be determined by a resonant frequency of EBC. Based on the above equations, we have designed EBC with constant ring-capacitor value under the conditions with resonant frequency of 63.86MHz (1.5T), N=22, a/b=1.15, a=375mm, and l_r = 500mm.

Simulations: Our own program³ which was based on the method of moments was used for numerical simulations. This program can calculate the B₁⁺ distribution generated by RF coil. The value of B₁⁺ in the numerical simulation was defined by the B₁⁺ field generated when a signal of 1W was fed to the coil.

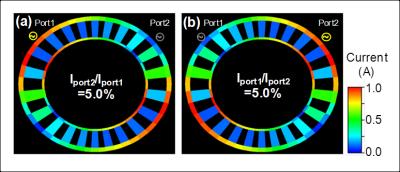
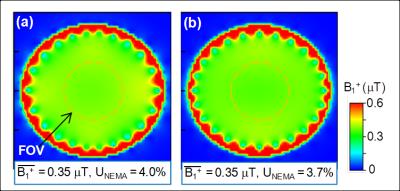
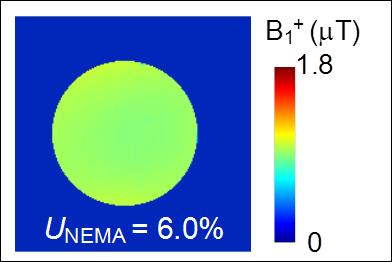
Evaluation: To confirm the resonant mode of the designed EBC, its current distribution was evaluated by numerical simulation. Isolation between two feeding ports of the EBC was also evaluated. To evaluate the uniformity of B₁⁺ distribution, B₁⁺ distribution of the designed EBC with quadrature drive (QD) was calculated under the unloaded condition. Uniformity of B₁⁺ distribution (U_NEMA) was evaluated with the NEMA standard. ⁵ The transmission efficiency of the designed EBC was compared to that of conventional EBC¹ under the same coil dimensions. We also fabricated the EBC with constant ring-capacitor value and acquired B₁⁺ map of cylindrical oil phantom (φ:300mm) using double angle method.⁴

Results & Discussion

Simulation results: Figure 2 shows the current distribution of the designed EBC. The ring current at the un-driven port showed the minimum value. Ratio of the current at Port #2 to that at Port #1 (I_port2/I_port1) was 5.0% in Fig. 2a. In Fig. 2b, I_port1/I_port2 was also 5.0%. These results indicated that the designed EBC had good isolation between two feeding ports. Figure 3 shows B₁⁺ distributions by the designed EBC and the conventional EBC at axial mid-plane of EBC, respectively. U_NEMA of B₁⁺ distribution by the designed EBC and the conventional EBC were 4.0% and 3.7% in the 30 cm FOV, respectively. These results indicated that there were no differences in B₁⁺ uniformity between the designed EBC and the conventional EBC. The averaged value of B₁⁺ distribution by the designed EBC and the conventional EBC was 0.35μT in the 30cm FOV. This result indicated that the transmission efficiency of the designed EBC was identical to that of the conventional EBC.

Experimental results: Figure 4 shows B₁⁺ map of cylindrical oil phantom at axial mid-plane. The uniform B₁⁺ distribution was acquired by the fabricated EBC with QD. B₁⁺ map of the oil phantom showed U_NEMA of 6.0% in the 30 cm FOV. It is considered that the difference in U_NEMA between simulation and experiment is caused by the fabrication error of the designed EBC.

Conclusion

Acknowledgements

References

1. S. Li, et. al., Magn. Reson. Med., Vol. 37, pp.600-608, (1997)

2. M.C. Leifer, Magn. Reson. Med., Vol. 38, pp.726-732, (1997)

3. H. Ochi, et al., SMRM 11th Annual Meeting, 4021 (1992)

4. Strollberger, Magn. Reson. Med., Vol. 35, pp.246-251, (1996)

5. NEMA Standard Publications. MS 1 (1988)